Предмет: Алгебра,
автор: swiftkey79
СРОЧНО 30 баллов! РЕШИТЕ СОВОКУПНОСТЬ НЕРАВЕНСТВ.
Тот, кто это решит настоящий гений
Приложения:
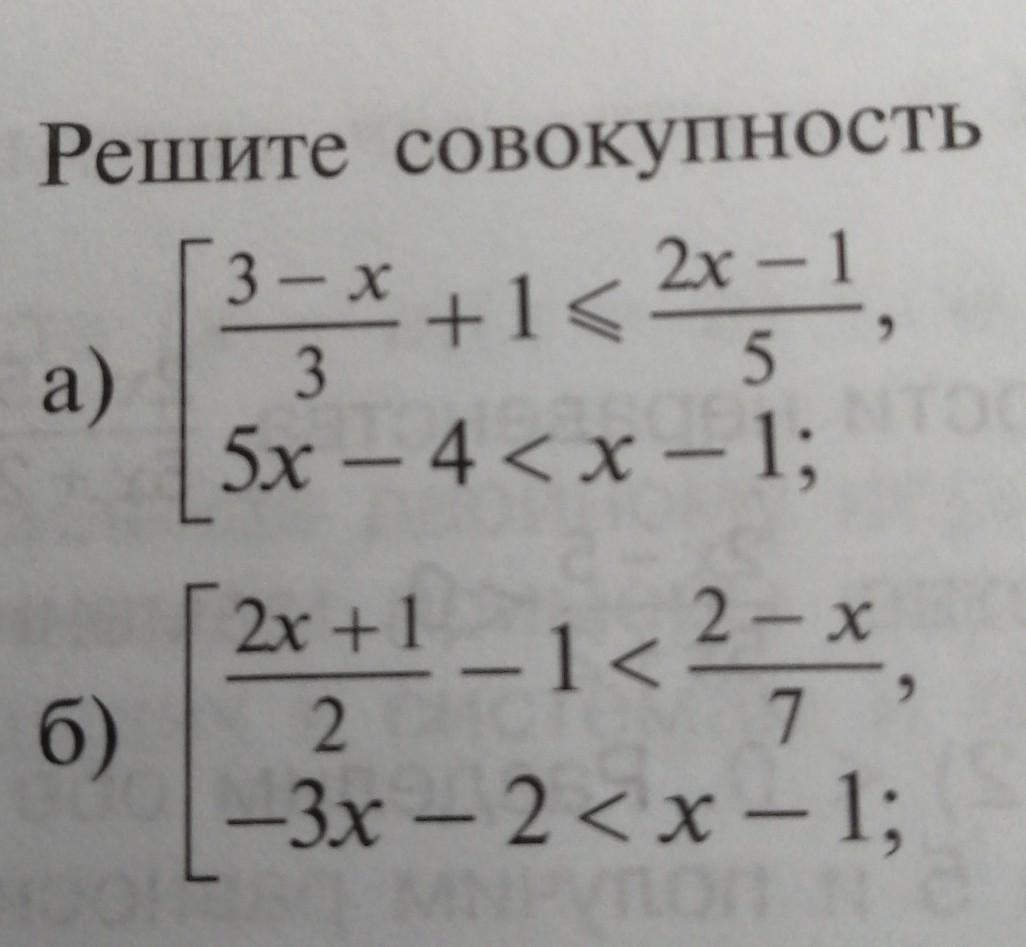
Ответы
Автор ответа:
1
Заданы совокупности неравенств, то есть в ответе надо находить объединение множеств, а не пересечение множеств, как при решении системы неравенств.
То есть нужно найти все такие значения переменной, каждое из которых является решением хотя бы одного из заданных неравенств.
Похожие вопросы
Предмет: История,
автор: ученица343
Предмет: Химия,
автор: школьница82
Предмет: Українська мова,
автор: ЯнусяБоднарчук
Предмет: Литература,
автор: afinaty4