Question

Найди радиус окружности, если расстояние от центра окружности до хорды равно 5, а длина хорды равна 24.

Answer 1

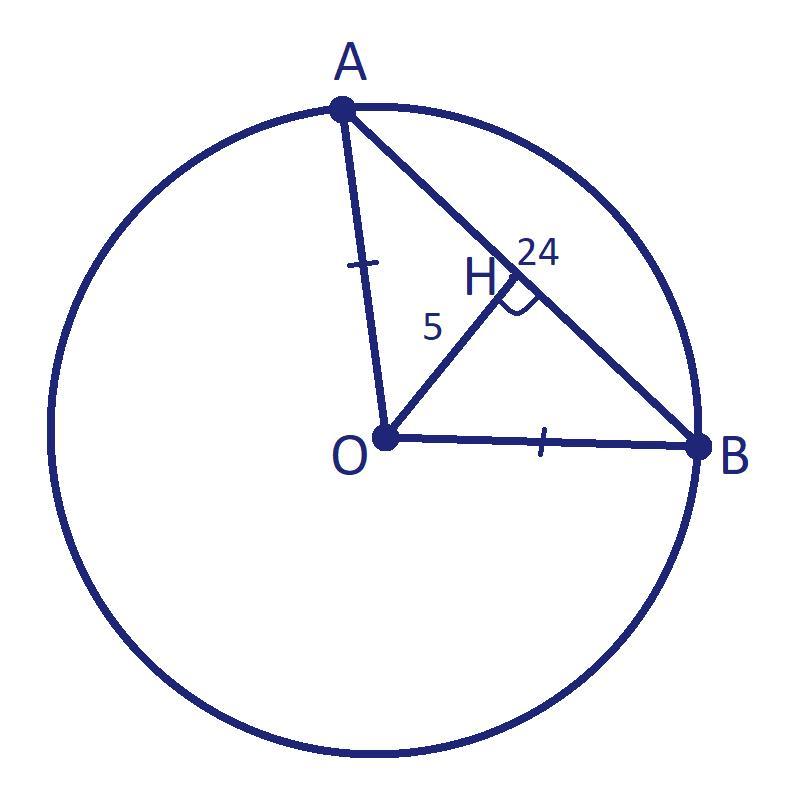
Пусть дана окружность с центром O и хорда AB = 24.

AO = BO, как радиусы одной окружности;

△AOB - равнобедренный т.к. AO=BO,

• Высота равнобедренного треугольника, проведённая к его основанию, является так же и медианой.

Пусть OH⊥AB, тогда OH - медиана △AOB.

OH = 5, как расстояние от O до AB.

HB = HA = AB:2 т.к. H - основание медианы;

HB = 24:2 = 12.

△OHB - прямоугольный (∠H=90°),

• Квадрат гипотенузы равен сумме квадратов катетов (т. Пифагора).

BO² = OH²+HB²;

BO² = 5²+12²;

BO² = 25+144;

BO² = 169 = 13²;

BO = 13 - радиус окружности.

Ответ: 13.