Решить систему линейных уравнений
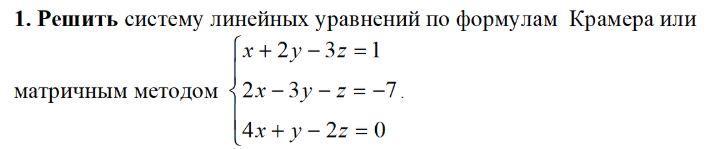
Ответы
Ответ:
Объяснение:
Решение на фото

Решение методом Крамера.
Воспользуемся формулой для вычисления определителя матрицы 3×3:
∆ = В
1 2 -3 1
2 -3 -1 -7
4 1 -2 0
= 1·(-3)·(-2) + 2·(-1)·4 + (-3)·2·1 - (-3)·(-3)·4 - 1·(-1)·1 - 2·2·(-2) =
= 6 - 8 - 6 - 36 + 1 + 8 = -35.
Заменяем 1-й столбец на вектор результатов B:
∆1 =
1 2 -3
-7 -3 -1
0 1 -2 =
= 1·(-3)·(-2) + 2·(-1)·0 + (-3)·(-7)·1 - (-3)·(-3)·0 - 1·(-1)·1 - 2·
·(-7)·(-2) = 6 + 0 + 21 - 0 + 1 - 28 = 0.
Заменяем 2-й столбец на вектор результатов B:
∆2 =
1 1 -3
2 -7 -1
4 0 -2 =
= 1·(-7)·(-2) + 1·(-1)·4 + (-3)·2·0 - (-3)·(-7)·4 - 1·(-1)·0 - 1·2·
·(-2) = 14 - 4 + 0 - 84 - 0 + 4 = -70.
Заменяем 3-й столбец на вектор результатов B:
∆3 =
1 2 1
2 -3 -7
4 1 0 =
= 1·(-3)·0 + 2·(-7)·4 + 1·2·1 - 1·(-3)·4 - 1·(-7)·1 - 2·2·0 =
= 0 - 56 + 2 + 12 + 7 - 0 = -35.
x = ∆1 / ∆ = 0 /-35 = 0.
y = ∆2 / ∆ = -70 / -35 = 2.
z = ∆3 / ∆ = -35 / -35 = 1.