Предмет: Геометрия,
автор: cambogiyt
Даны координаты вершин пирамиды А1А2А3А...
Приложения:
Ответы
Автор ответа:
0
Задача: Даны координаты вершин пирамиды: A₁A₂A₃A₄: A₁(7, 2, 4), A₂(7, −1, −2), A₃(3, 3, 1), A₄(−4, 2, 1). Найти площадь грани A₁A₂A₄.
·······························································
Ответ: Площадь грани A₁A₂A₄ равна 37 квадратным единицам.
Автор ответа:
0
Решеие смотрите во вложении
Приложения:
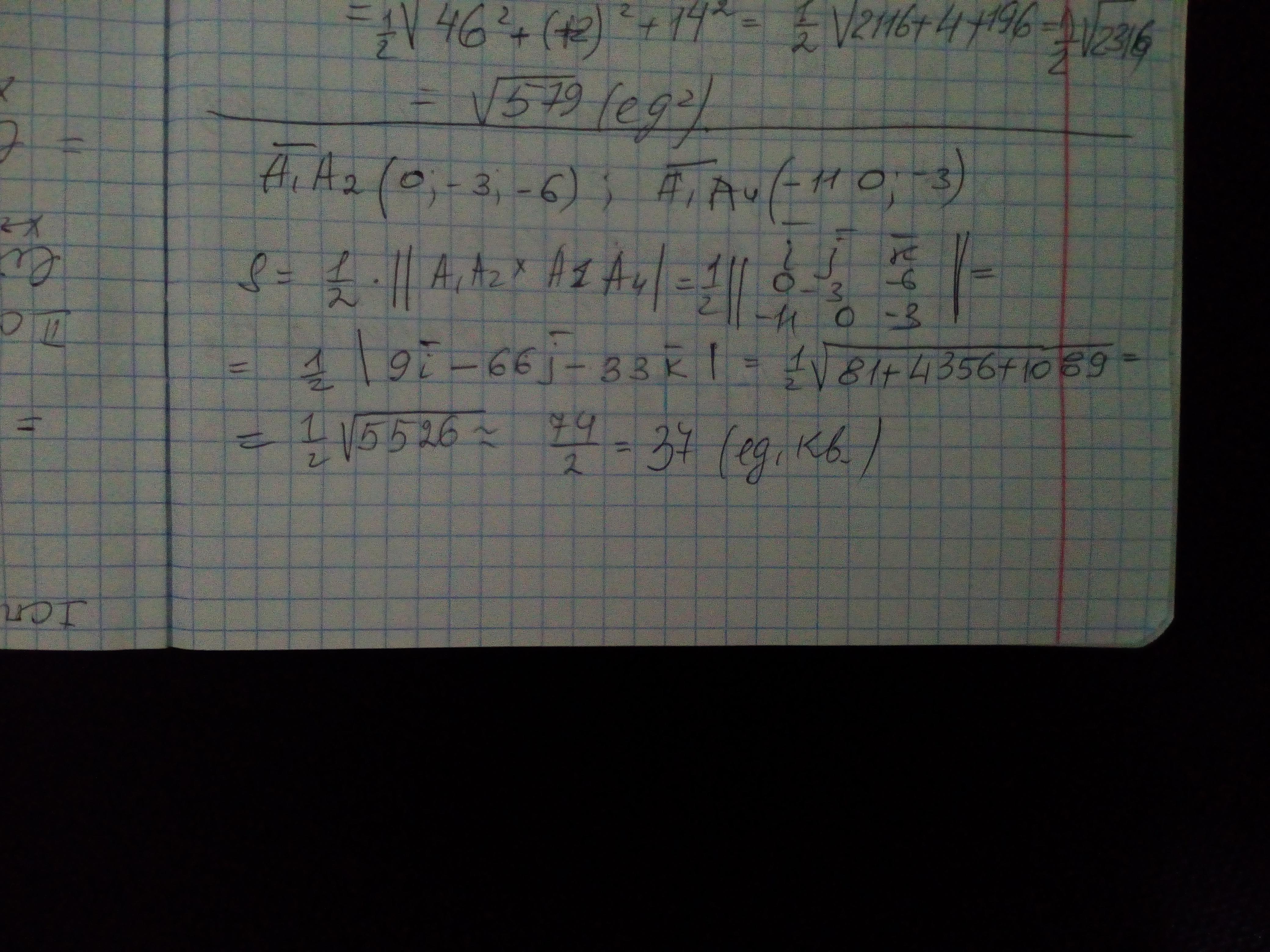
Похожие вопросы
Предмет: Английский язык,
автор: ychebnik287
Предмет: Русский язык,
автор: angel566
Предмет: Русский язык,
автор: Kristina30041995
Предмет: Математика,
автор: Кам111111
Предмет: Математика,
автор: ЕрнарЖанар