Предмет: Алгебра,
автор: zil21
Помогите решить пожалуйста
Приложения:
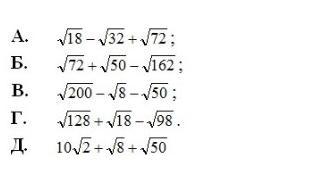
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Українська мова,
автор: Igor353
Предмет: Английский язык,
автор: Vikssss
Предмет: Русский язык,
автор: ds67
Предмет: Химия,
автор: Dianak03
Предмет: Математика,
автор: fedorvarlamov