Предмет: Алгебра,
автор: Dima31355
ПОМОГИТЕ СРОЧНО! !!!!
Скільки разів у сумі під знаком кореня необхідно записати число 2018вквадрате, щоб рівність
ДАЙТЕ ПОЖАЛУЙСТА РАЗВЕРНУТОЕ РЕШЕНИЕ11
Приложения:
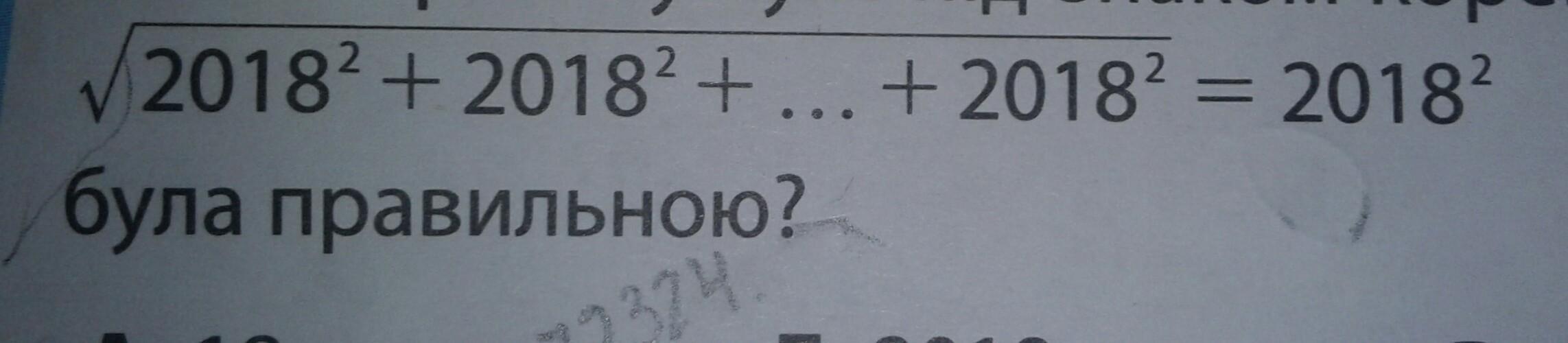
Ответы
Автор ответа:
1
Ответ:
2018²
Объяснение:
По свойству квадратного корня правую часть равенства можно представить как
, тогда получим
, следовательно подкоренные выражения равны, т.е.
Сумму одинаковых чисел всегда можно представить в виде произведения этого числа на количество раз, которое оно присутствует в сумме, например 5 + 5 + 5 = 3*5, 7+7+7+7 = 4*7.
Представим в виде произведения:
, тогда найдя n получим ответ на вопрос.
Похожие вопросы
Предмет: Русский язык,
автор: milaLLlka
Предмет: Русский язык,
автор: zoya01
Предмет: Другие предметы,
автор: 7Маша2
Предмет: Математика,
автор: JuliaKuki
Предмет: Математика,
автор: Аноним