Предмет: Алгебра,
автор: umnicka51
СРОЧНО ПОМОГИТЕ ЭТО РЕШИТЬ .
Приложения:
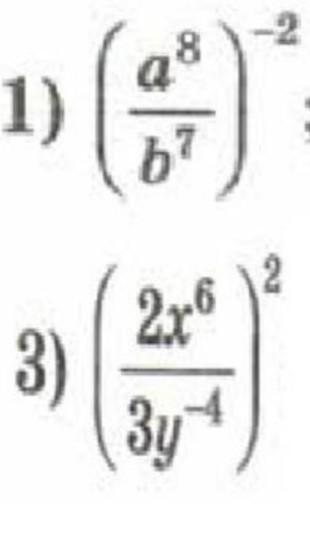
Ответы
Автор ответа:
0
umnicka51:
по какой формуле вы решали??
возведение дроби в степень...
поняла , спасибо
написала правило....
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: максb
Предмет: Українська мова,
автор: dana2000hnidets
Предмет: Химия,
автор: karatere