Предмет: Алгебра,
автор: mtopychkanova
срочно помогите 30 баллов!!!(договоримся)
пожалуйста
решить дифференциальное уравнение
y’=2^(x-y)
Приложения:
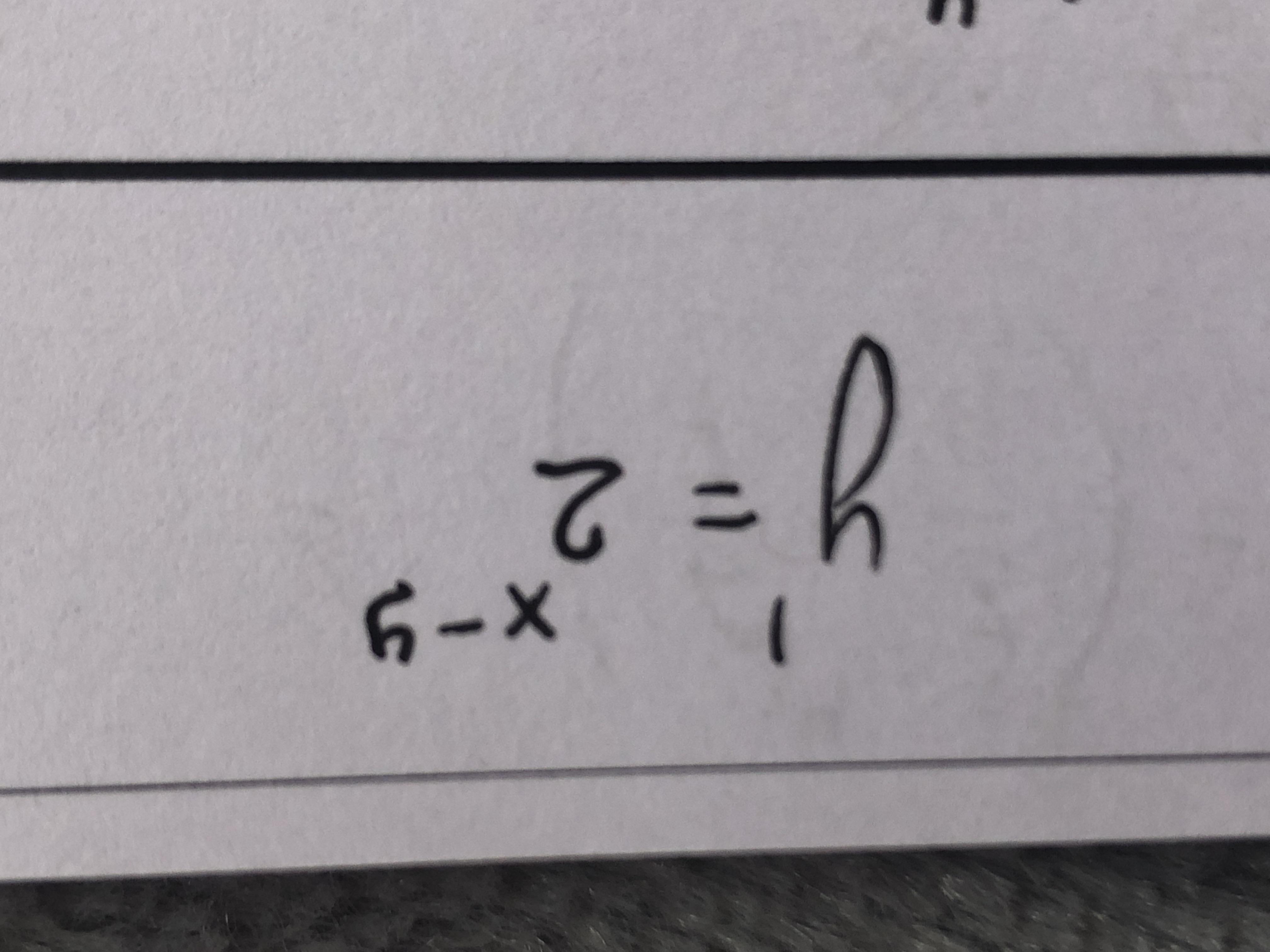
Ответы
Автор ответа:
2
Похожие вопросы
Предмет: Қазақ тiлi,
автор: BuGaTTi001
Предмет: Другие предметы,
автор: Лисёнок9
Предмет: Английский язык,
автор: lars01
Предмет: Математика,
автор: alinazinnatullina
Предмет: Физика,
автор: Елизавета19992000