Предмет: Алгебра,
автор: katerinabogomaz2000
Обчислити площу фігури(інтеграли)
35 балів
Приложения:
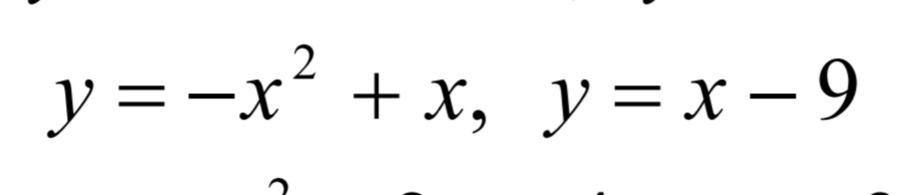
Ответы
Автор ответа:
1
Щоб знайти межі інтегрування, знайдемо точки, де дані дві функції перетинаються:
Знаходимо площу:
Відповідь: 36 кв. од.
katerinabogomaz2000:
А графіком функції буде парабула та пряма?
Да
Парабола с ветвями направленными вниз
Спасибо большое))
Пожалуйста)
Привет, тама в профиле задание,можешь посмотреть пожалуйста)
Похожие вопросы
Предмет: Қазақ тiлi,
автор: liliyasag
Предмет: Русский язык,
автор: АиДоска
Предмет: Русский язык,
автор: Хчиль
Предмет: Биология,
автор: Аноним