Предмет: Алгебра,
автор: fir2103
№4. Срочно!.........
Приложения:
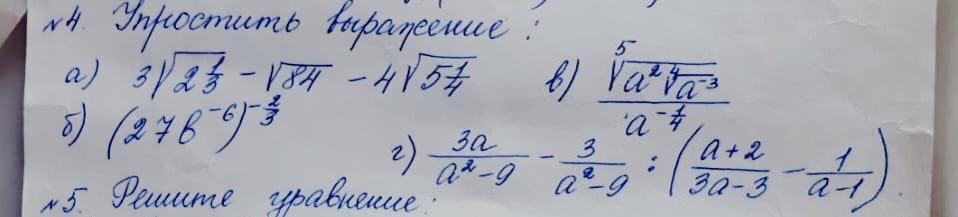
Ответы
Автор ответа:
1
a)
б)
в)
г)
Похожие вопросы
Предмет: Русский язык,
автор: 9Anastasiya9
Предмет: Русский язык,
автор: 28061981
Предмет: Английский язык,
автор: Gulehka
Предмет: История,
автор: Вероникka
Предмет: Литература,
автор: egadr