Предмет: Алгебра,
автор: dasik2016
Решите Линейные дифференциальные уравнения.Задание 5.3
Приложения:
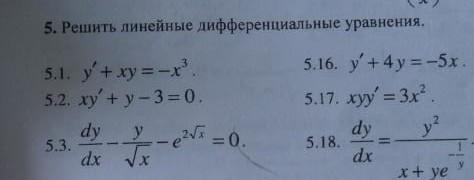
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: frag2108
Предмет: Английский язык,
автор: albinaby
Предмет: Русский язык,
автор: КирИлОв
Предмет: Математика,
автор: диана1786
Предмет: Математика,
автор: Аноним