Question

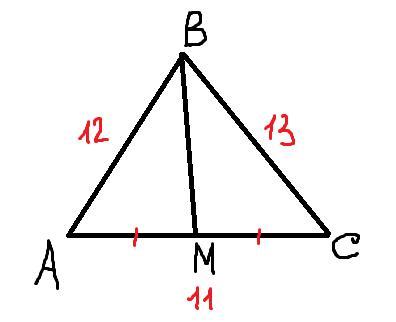
Три стороны треугольника равны 11 см, 12 см и 13 см . найти медиану проведенную к меньшей стороны

Answer 1

Пусть АВ = 12 см, ВС = 13 см, АС = 11 см.

Проведем медиану к меньшей стороне ВМ. Так как М - середина АС, то отрезки АМ = МС = 11 см : 2 = 5.5 см.

Запишем теорему косинусов для треугольника АВС:

$BC^2=AB^2+AC^2-2AB\cdot AC\cdot\cos A$

Выразим косинус угла А:

$2AB\cdot AC\cdot\cos A=AB^2+AC^2-BC^2$

$\cos A=\dfrac{AB^2+AC^2-BC^2}{2AB\cdot AC}$

Запишем теорему косинусов для треугольника АВM:

$BM^2=AB^2+AM^2-2AB\cdot AM\cdot\cos A$

Подставим выражение для косинуса:

$BM^2=AB^2+AM^2-2AB\cdot AM\cdot\dfrac{AB^2+AC^2-BC^2}{2AB\cdot AC}$

$BM^2=AB^2+AM^2-\dfrac{AM}{AC}\cdot(AB^2+AC^2-BC^2)$

$BM^2=12^2+5.5^2-\dfrac{5.5}{11}\cdot(12^2+11^2-13^2)$

$BM^2=144+30.25-\dfrac{1}{2}\cdot(144+121-169)$

$BM^2=174.25-\dfrac{1}{2}\cdot96$

$BM^2=126.25$

$BM=\sqrt{126.25} =\dfrac{\sqrt{505}}{4}$

Ответ: $\dfrac{\sqrt{505}}{4}$ см