Question

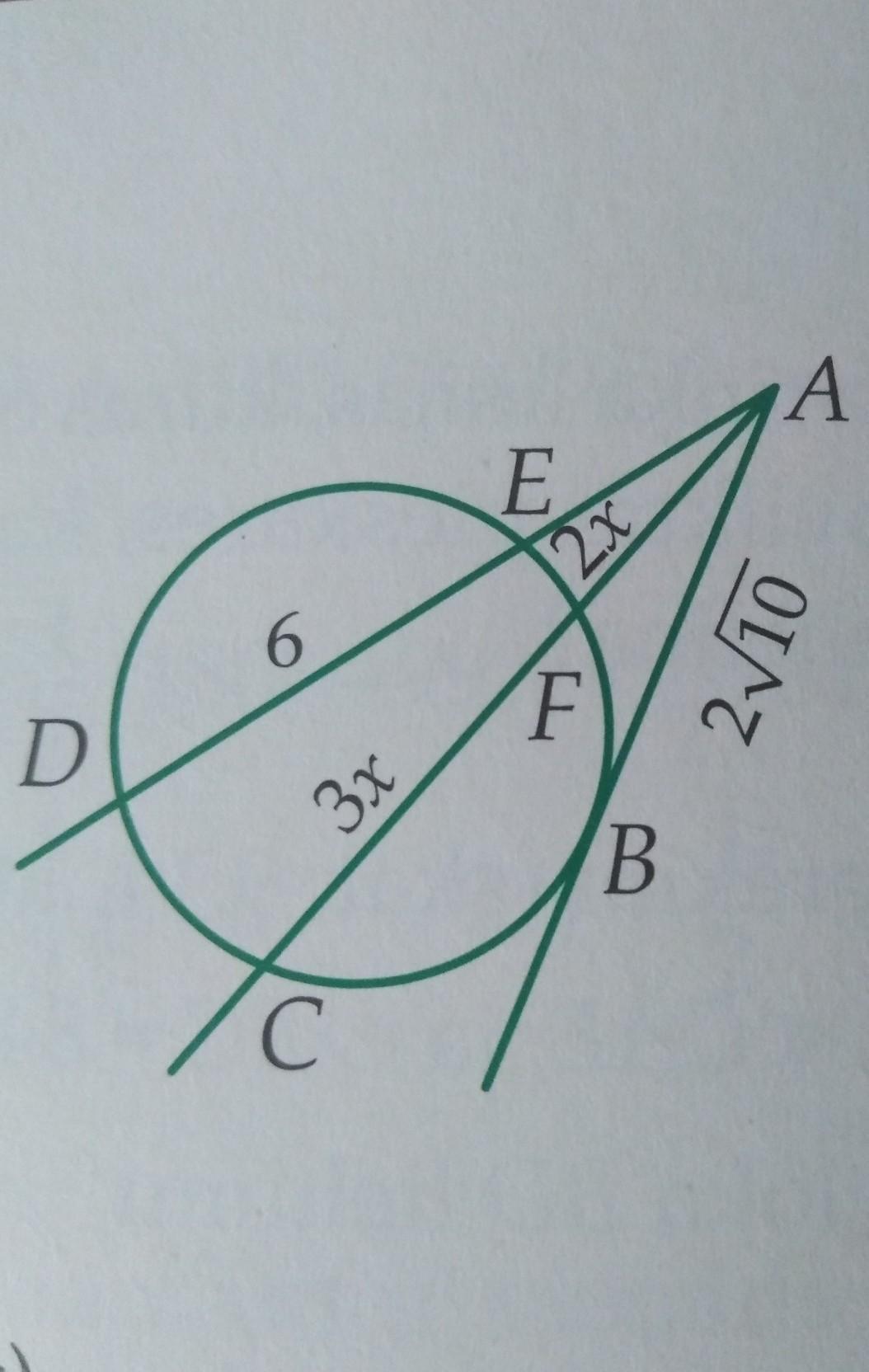
За пределами круга есть точка A. Касательная AB проходит через точку A, и два преемника AC и AD пересекают круг в точках F и E соответственно (см. Рисунок 9.20). Известно, что AB = 2/10 см, DE = 6 см, но CF: FA = 3: 2. Расчеты длин секций AC и AD.​

Answer 1

Ответ:

AC = 10

AD = 10

Пошаговое объяснение:

AF * AC = AB^2 (теорема о квадрате касательной)

2x * 5x = (2√10)^2

10x^2 = 40

x = 2, значит, AC = 5x = 10

AE * AD = AB^2 (теорема о квадрате касательной)

Обозначим t = AE, получается:

t * (t + 6) = 40

t^2 + 6t - 40 = 0

(t + 10)(t - 4) = 0

t = 4 (т. к. t > 0)

AD = AE + DE = t + 6 = 10