Предмет: Алгебра,
автор: favaj44624
Проинтегрировать дифференциальное уравнение:
Приложения:
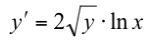
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Українська мова,
автор: Vova0804
Предмет: Русский язык,
автор: элиза000
Предмет: Английский язык,
автор: Кристина130276
Предмет: Математика,
автор: bakieva802
Предмет: Математика,
автор: РомаРил