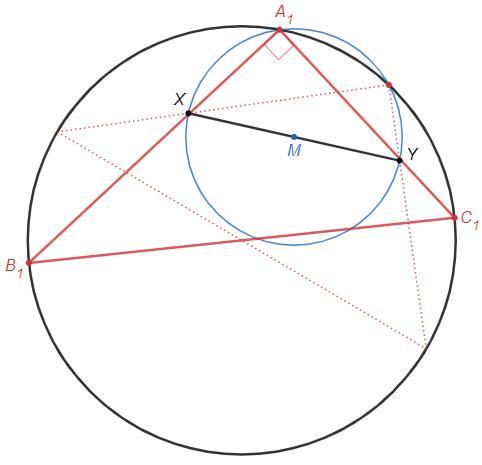
Требуется построить прямоугольный треугольник, вписанный в данную окружность так, чтобы его катеты проходили через две заданные точки. Укажите одно или несколько ГМТ, которые потребуются для построения.
ГМТ, находящихся на заданном расстоянии от данной точки
ГМТ, находящихся на заданном расстоянии от данной прямой
ГМТ, равноудаленных от двух точек
ГМТ, равноудаленных от двух параллельных прямых
ГМТ, равноудаленных от двух пересекающихся прямых
ГМТ, из которых данный отрезок виден под прямым углом
Ответы
Дана окружность и точки X и Y внутри нее.
Ответ:
На отрезке XY как на диаметре построим окружность. Пересечения построенной окружности с данной окружностью - вершины треугольника (A1, A2).
Объяснение:
1) Построим середину отрезка XY - точку M.
(Для этого построим серединный перпендикуляр к отрезку:
- две дуги с центрами в концах отрезка
- прямую через точки пересечения дуг
Прямая пересечет отрезок в его середине)
Серединный перпендикуляр к отрезку - ГМТ, равноудаленных от двух точек.
2) Построим окружность с центром M радиусом MX.
Пересечение построенной окружности с данной окружностью - вершина А1 искомого треугольника.
Вписанный угол A1 - прямой, т.к. опирается на диаметр XY.
Окружность - ГМТ, из которых данный отрезок (диаметр) виден под прямым углом.
3) Проведем прямые A1X и A1Y. Их пересечения с данной окружностью - вершины B1 и С1 искомого треугольника.
Аналогично строим вершины B2 и С2, если имеется точка A2.