Предмет: Математика,
автор: DiGray1
Проинтегрировать дифференциальное уравнение.
Приложения:
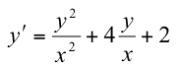
Ответы
Автор ответа:
1
Это линейное однородное дифференциальное уравнение первого порядка. Для этого уравнения всегда осуществляется замена , тогда
, получаем :
Получили дифференциальное уравнение с разделяющимися переменными.
Выполним обратную замену
Получили общее решение диф. уравнения.
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: MILKAZ
Предмет: Українська мова,
автор: laram
Предмет: Українська мова,
автор: AllnA
Предмет: Математика,
автор: jansi1
Предмет: Математика,
автор: VaDяS