Предмет: Геометрия,
автор: nurlybek1
Помогите решить,желательно с рисунком
Приложения:
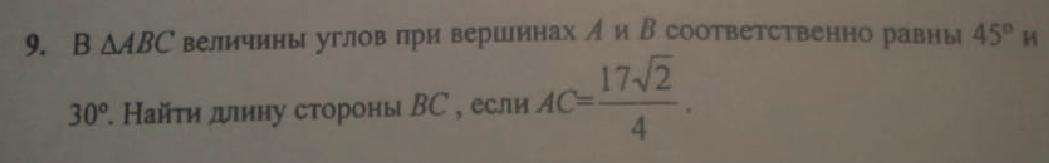
Ответы
Автор ответа:
1
Задача: ΔABC величины углов A и B соответственно равны 45° и 30°. Найти длину стороны BC, если AC = .
Решение:
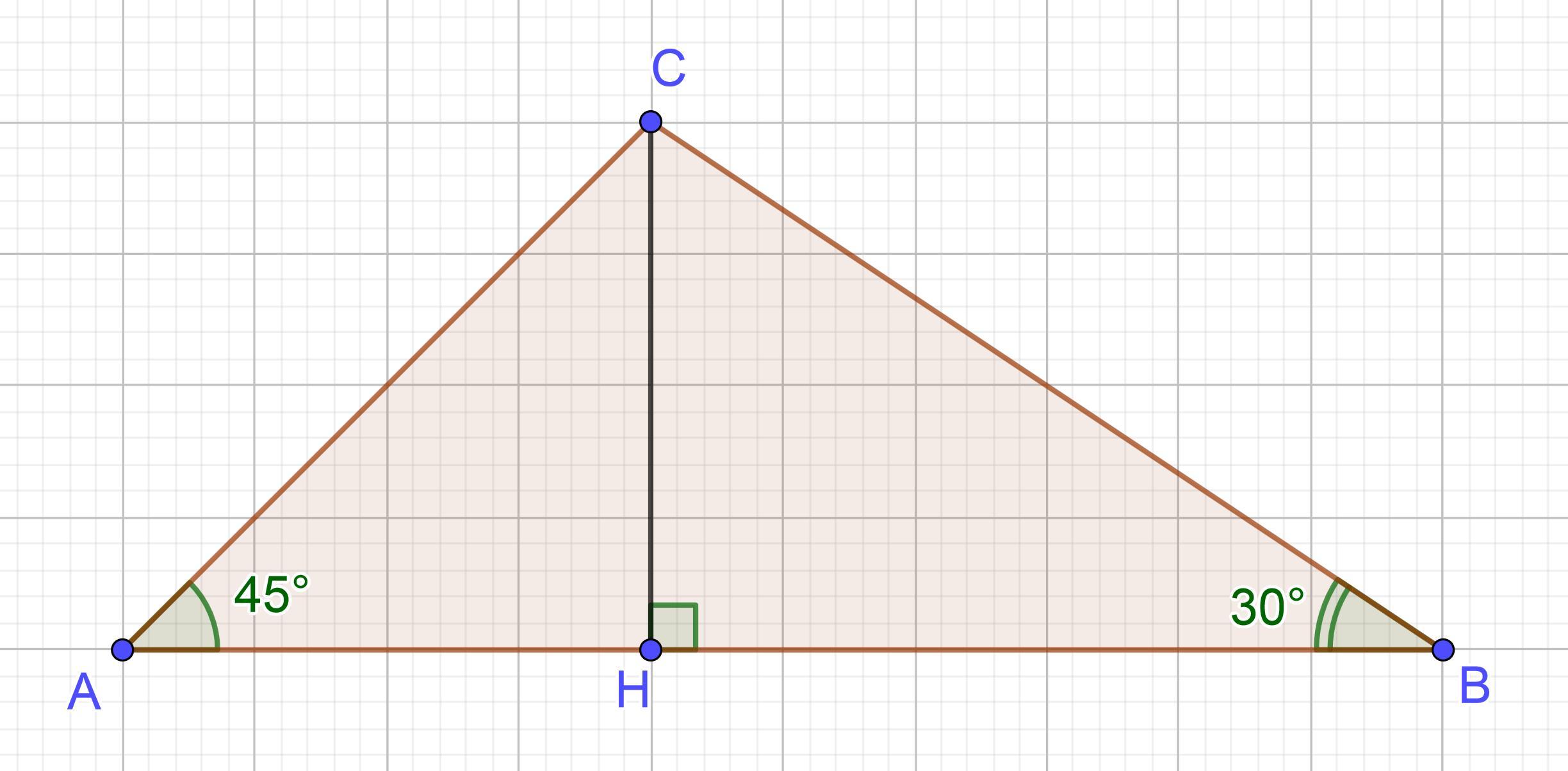
Проведем из вершины C на сторону AB высоту CH: получим два прямоугольных треугольника — ACH и BCH.
Воспользуемся тригонометрическими свойствами углов в прямоугольном треугольнике:
Найдем общий катет CH, рассмотрев ΔACH:
Р-м ΔACH BCH:
По свойству катета, лежащего против угла 30°, гипотенуза BC (искомая сторона) будет равна:
Ответ: Длина стороны BC равна 8,5.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: winuser
Предмет: Другие предметы,
автор: Надя89522079613
Предмет: Русский язык,
автор: Аноним
Предмет: Литература,
автор: lizanesterova71
Предмет: Математика,
автор: катя3545