Предмет: Математика,
автор: grg5tgtre
Отдаю все балы помогите прошу..
Приложения:
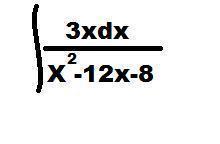
Ответы
Автор ответа:
1
Неопределённый интеграл
=================================
Использованы табличные интегралы
Похожие вопросы
Предмет: Английский язык,
автор: lindalinda1999
Предмет: Английский язык,
автор: Аноним
Предмет: Українська мова,
автор: ромео57
Предмет: Математика,
автор: олег619
Предмет: Математика,
автор: янаберкат