Предмет: Математика,
автор: borodinaalexsa
Найти определённый интеграл
Приложения:
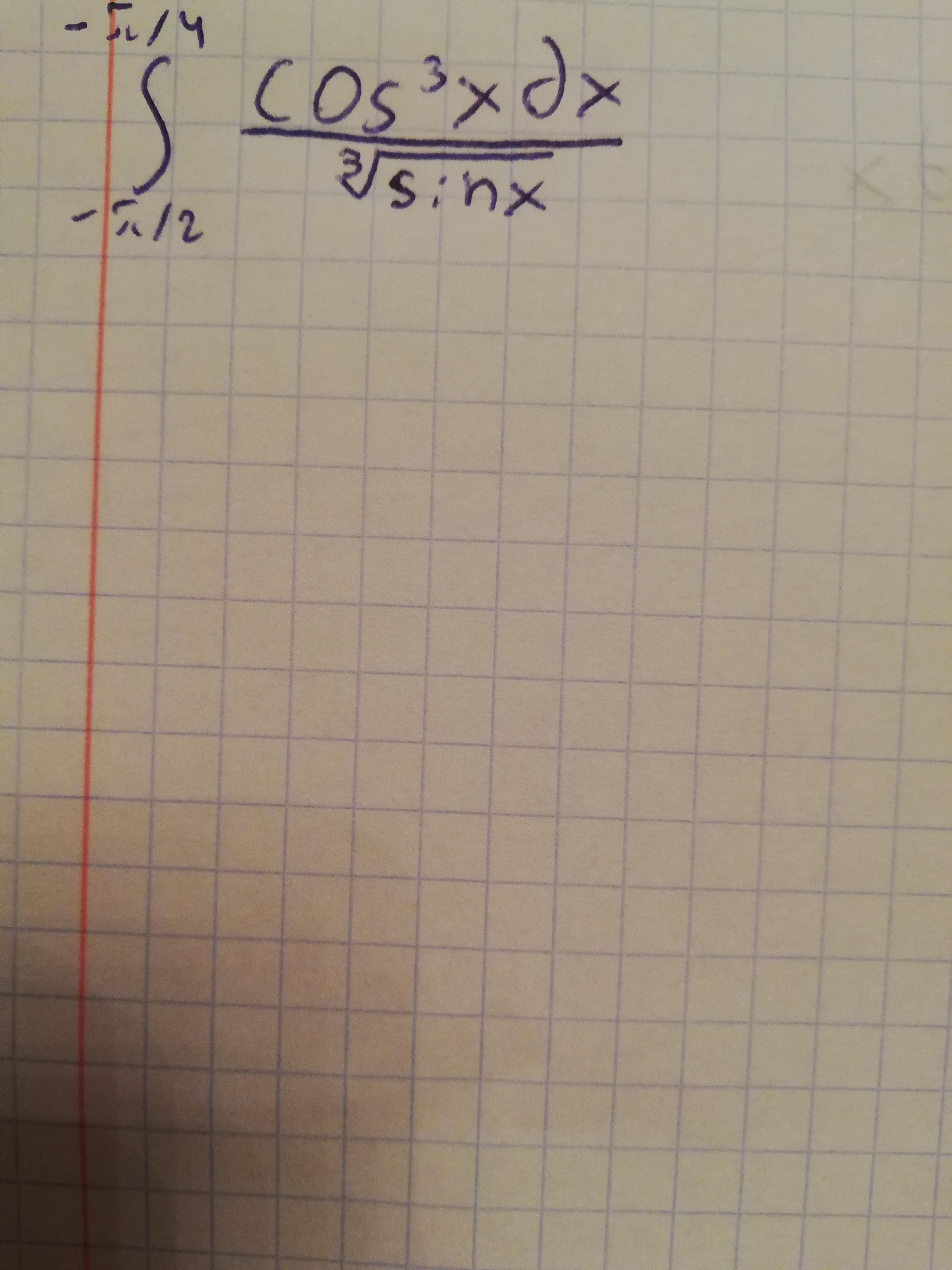
Ответы
Автор ответа:
0
Дальше считайте как хотите. Можно без комплексов:
Ответ в комплексах такой:
Похожие вопросы
Предмет: Русский язык,
автор: umnaxa
Предмет: Русский язык,
автор: goacat
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: bogatova2005