Question

решите пожалуйста. желательно все. дам 50 баллов.

Answer 1

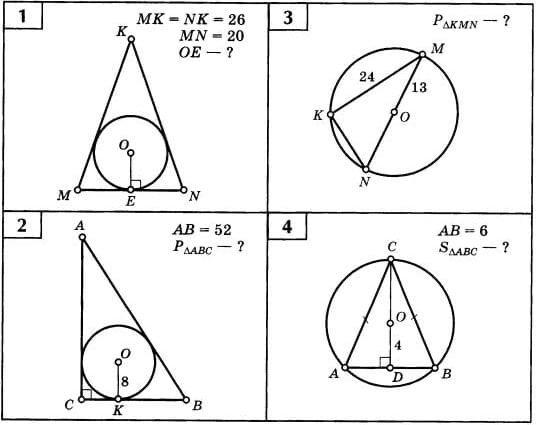
1) Воспользуемся формулой S = pr, где r = OE, p - полупериметр треугольника. Отсюда r = S/p.

p =(MK + NK + MN) : 2 = (26 + 26 + 20) : 2 = 36.

Площадь находим по формуле Герона:  $S=\sqrt{p(p-a)(p-b)(p-c)}=\sqrt{36(36-26)(36-26)(36-20)}=6\cdot10\cdot4=240$

Тогда $r=\frac{240}{36} =6\frac{2}{3}$

2) Вписанный угол MKN опирается на диаметр окружности,а значит он - прямой, т.е. треугольник KMN прямоугольный с гипотенузой MN = 2MO = 26.

$KN=\sqrt{MN^2-KM^2}= \sqrt{26^2-24^2}=10$ - по следствию из теоремы Пифагора. Тогда $P_{MNK}=26+24+10=60$

3) OK - радиус вписанной окружности прямоугольного треугольника - находится по формуле $r=\frac{a+b-c}{2}$, где a,b - катеты, c - гипотенуза.

$8=\frac{a+b-52}{2}\Leftrightarrow 16=a+b-52\Rightarrow a+b=68$

Сумма катетов равна 68. Тогда $P = a+b+c=68+52=130$

4) CD - медиана и высота равнобедренного треугольника. По свойству медианы CO : OD = 2 : 1 ⇒ CO = 2OD = 8.

Тогда CD = h = 8 + 4 = 12.

S = 1/2 ah = 1/2 · 6 · 12 = 36.