Question

Площа трикутника АВС дорівнює 98 см2. Точка К поділяє його медіану BM у відношенні
4:3, рахуючи від точки В. Зайдіть площі трикутників ABK, BKC, CKM i AKM.

Answer 1

Ответ:

$S_{AKM}=S_{MKC}=21(cm^2)$

$S_{ABK}=S_{KBC}=28(cm^2)$

Объяснение:

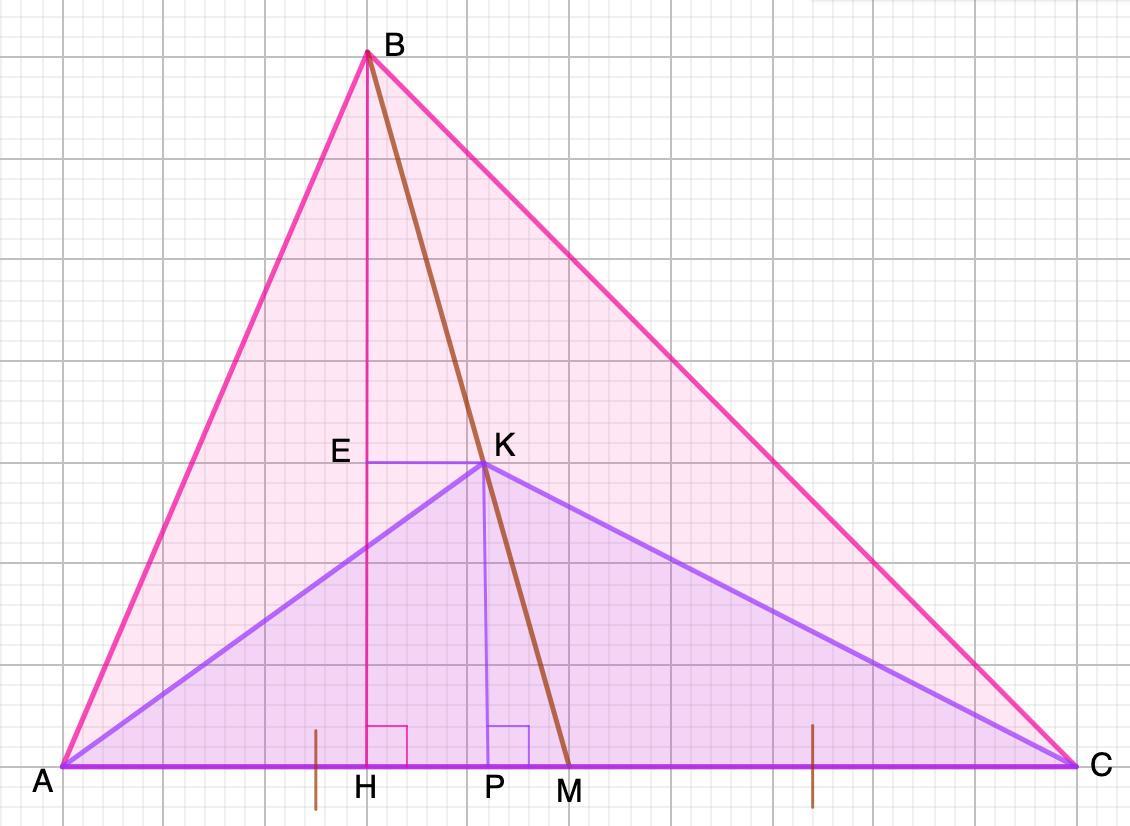
Дано: ΔАВС;

$S_{ABC}=98cm^2$;

ВМ - медиана;

ВК:КМ=4:3

Найти:

$S_{ABK};\;\;\;S_{BKC};\;\;\;S_{CKM};\;\;\;S_{AKM}.$

Решение:

Медиана делит треугольник на два равновеликих треугольника.

Дополнительное построение:

ВН и КР - высоты; КЕ║АС.

1. Согласно правилу:

$S_{ABM}=S_{MBC}=98:2=49(cm^2)\\S_{AKM}=S_{MKC}$

⇒ $S_{ABK}=S_{KBC}$

2. Рассмотрим ΔНВМ и ΔЕВК.

ЕК║НМ ⇒ΔНВМ ~ ΔЕВК (лемма о подобии треугольников)

$\frac{BK}{BM}=\frac{EB}{BH}= \frac{4}{4+3}=\frac{4}{7}$

3. Пусть ВН=7х см, тогда ЕВ=4х см ⇒ЕН=КР=3х см.

$S_{ABC}=\frac{1}{2} AC*7x=98 (cm^2)\\AC*x=28 (cm^2)\\S_{AKC}=\frac{1}{2} AC*3x=\frac{3}{2} *( AC*x)=\frac{3}{2} *28=42 (cm^2)$

4. Найдем искомые площади:

$S_{AKM}=S_{MKC}=S_{AKC}:2=21(cm^2)$

$S_{ABK}=S_{KBC}=49-21=28(cm^2)$