Question

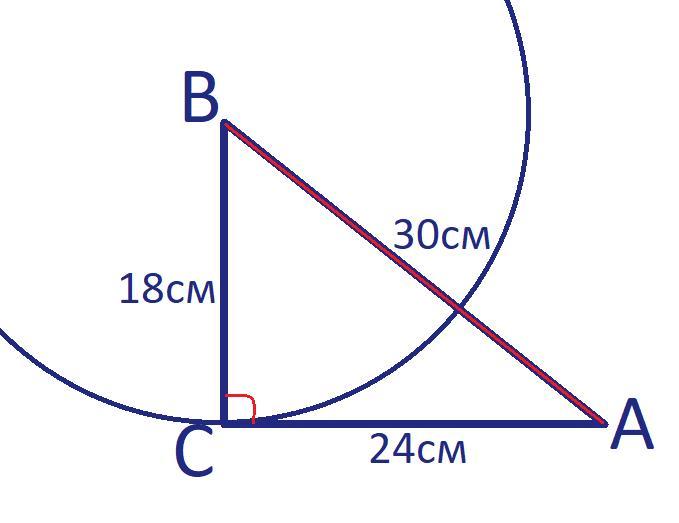
В треугольнике АВС известны стороны АВ = 30 см, ВС = 18 см и АС = 24 см. Сколько общих точек имеет окружность с центром в точке В и радиусом 18 см со стороной АС?

Answer 1

Ответ: 1.

Объяснение:

Заметим, что

AB² = (30см)² = (6·5см)² = 36·25см²;

BC²+AC² = (18см)²+(24см)² = (6·3см)²+(6·4см)² = 36·(9+16)см²;

BC²+AC² = 36·25см² = AB².

• Если квадрат одной стороны равен сумме квадратов двух других, то треугольник является прямоугольным (обратная т. Пифагора).

⇒ △ABC - прямоугольный, при этом прямой угол против большей стороны;

BC < AC < AB ⇒ ∠BCA = 90°.

• Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна ему, то эта прямая является касательной.

Радиус окружности (B, 18см) равен стороне BC; AC∩BC=C - точка окружности; BC⊥AC

⇒ AC - касательная к окружности, значит всего 1 общая точка - С.

Сторона AC - отрезок касательной, тоже имеет всего 1 общею точку с окружностью (B, 18см).