помогите с уравнением
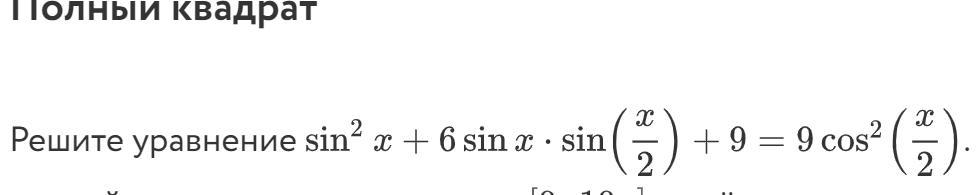
Ответы
Ответ:
Пошаговое объяснение:
Перенесем все в левую часть ур. , сгруппируем 2 последних слагаемых и свернем по формуле;
sin^2 x + 6sinx sinx/2 + 9sin^2x/2 = 0, (sinx + 3sinx/2)^2 = 0, sinx + 3sinx/2 = 0, 2sinx/2 cosx/2 + 3sinx/2 = 0,
sinx/2(2cosx/2 + 3) = 0, sinx/2 = 0 и cosx/2 = -3/2 - посторонний, тк. | - 3/2 | > 1. X/2 = Пк, х = 2Пк (к = 0; +-1; +-2; +-3...)
sin²x+6sinx*sin(x/2)+9=9cos²(x/2)
По формуле cos²(x/2)=1-sin²(x/2) заменим правую часть. получим
sin²x+6sinx*sin(x/2)+9=9*(1-sin²(x/2))
раскроем скобки в правой части, потом соберем все слева.
sin²x+6sinx*sin(x/2)+9=9-9sin²(x/2)
sin²x+6sinx*sin(x/2)+9-9+9sin²(x/2)=0⇒sin²x+6sinx*sin(x/2)+9sin²(x/2)=0
воспользуемся формулой а²+2аb+b²=(a+b)², где a=sinx; b=3sin(x/2),
свернем по формуле ((sinx+3sin(x/2))²=0, квадрат выражения равен нулю, если само выражение нуль, т.е. sinx+3sin(x/2)=0
По формуле двойного угла заменим sinх=2 sin(х/2)*cos(х/2),
sinх+3sin(x/2)=0
2 sin(х/2)*cos(х/2)+3sin(x/2)=0
вынесем sin(x/2) за скобки, получим sin(х/2)*(2cos(х/2)+3))=0
произведение равно нулю, когда хотя бы один множитель нуль. Если sin(х/2)=0, то х/2=πn; n∈Z, откуда х=2πn: n∈Z
Скобка же (2cos(х/2)+3))≠0, иначе косинус будет равен -1.5, а этого быть не может, т.к. -1 ≤cos(х/2)≤1.
Ответ х=2πn: n∈Z