Предмет: Математика,
автор: tetradruckovna
найти неопределенный интеграл способом подстановки
Приложения:
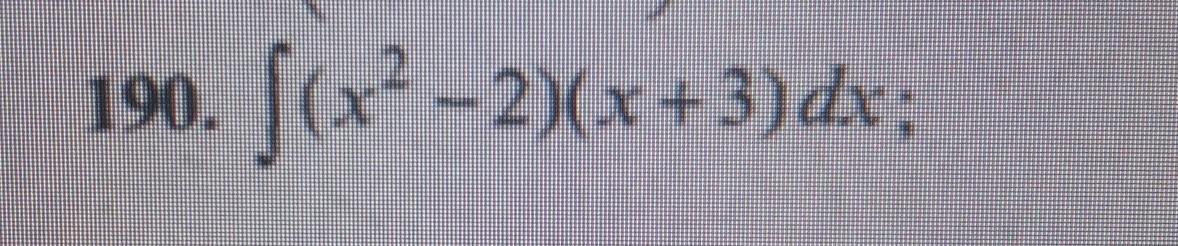
Ответы
Автор ответа:
1
Странное задание, если честно:
tetradruckovna:
откуда 7?
x^2-2=x^2-9+9-2=(x^2-9)+7=(x-3)(x+3)+7
откуда 9?
ааа
до меня дошло все
СПАСИБО
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: катюшкамото
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: знания86
Предмет: Математика,
автор: tolikkrytouychenik