Предмет: Математика,
автор: kefey72536
Высшая математика. Неопределенный интеграл
Приложения:
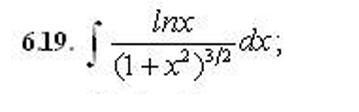
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: bola131
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: AnyaHurts
Предмет: Математика,
автор: Алина150508