Question

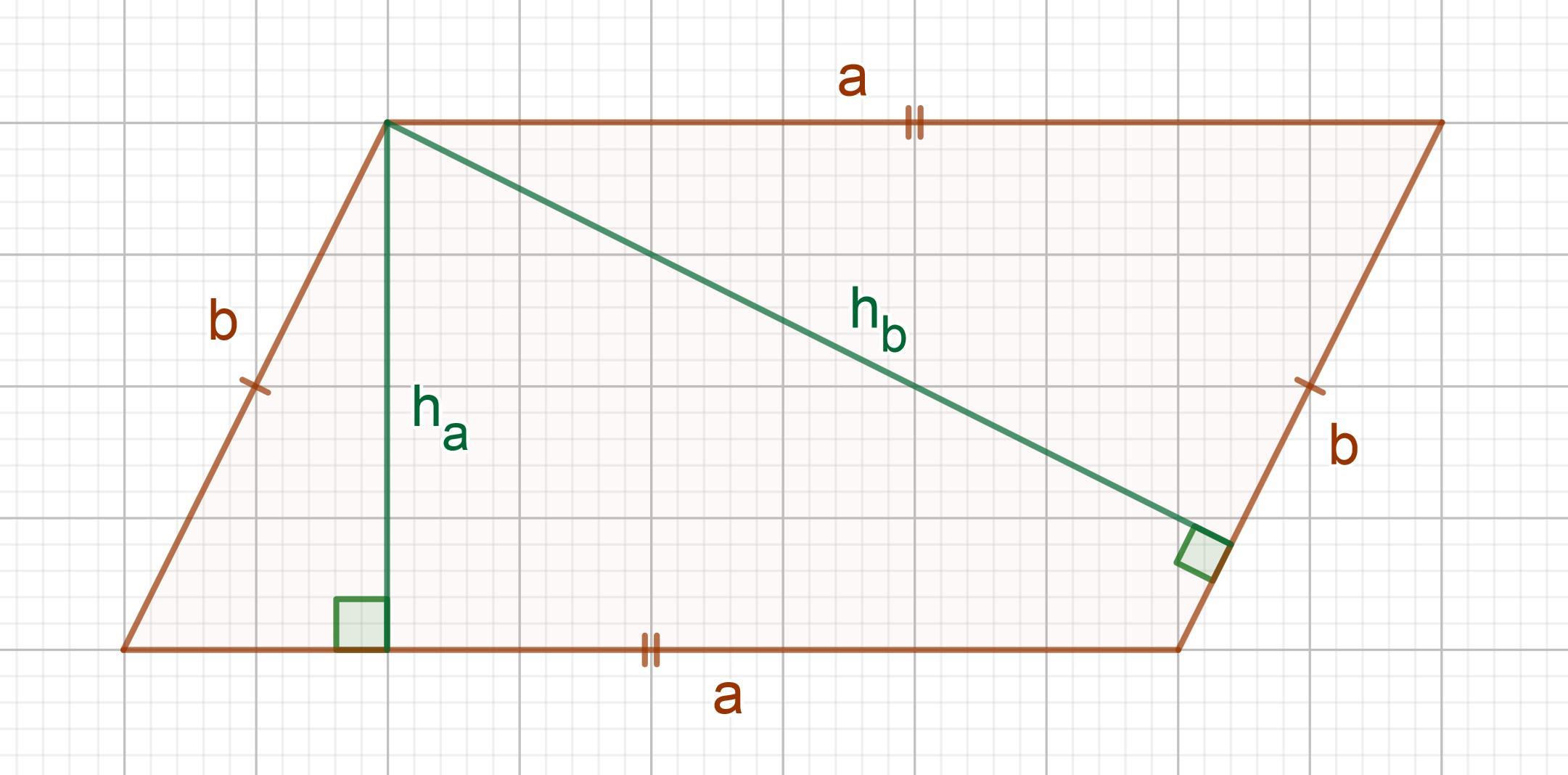
Высоты параллелограмма, опущенные из одной вершины, равны 12см и 18см. Одна из его сторон равна 30см. Найдите другую сторону параллелограмма.

Answer 1

Это решается через площадь.

Пусть первая сторона - a1, вторая сторона- a2. Первая высота - h1, вторая - h2.

В первом случае площадь параллелограмма равна a1 * h1

Во втором случае - a2 * h2

Площадь равна 12 * 30 = 360см^2

Подставляем во второй случай:

360= h2 * a2

Выражаем a2 : 360/18 = 20 см

Надеюсь, это лучший ответ)

Answer 2

Обозначим стороны параллелограмма за a и b, высоты за hᵃ и hᵇ, и:

a = 30 см,  hᵃ = 12 см, hᵇ = 18 см.

Формула площади параллелограмма:

S = a·hᵃ, a — сторона параллелограмма, hᵃ — высота, опущенная на сторону a.

Подставим значения и найдем площадь данного параллелограмма:

S = 30·12 = 360 (см²)

Воспользуемся формулой площади для нахождения второй стороны параллелограмма:

S = b·hᵇ ⇒ b = S/hᵇ

b = 360/18 = 20 (см)

Ответ: Другая сторона параллелограмма равна 20 см.