Question

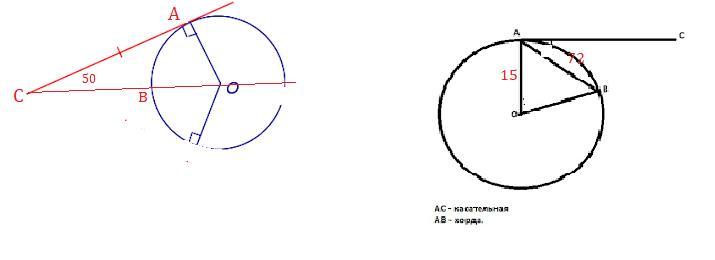
1) Через точку С, лежащую вне окружности с центром в точке О, проведена касательная АС к этой окружности, так что угол АСО=50 градусов. Найдите градусную меру меньшей дуги АВ, где В- точка пересечения отрезка ОС и окружности.

2. В окружности радиуса 15 с центром О проведена хорда АВ. Данная хорда стягивает дугу окружности в 72 градуса.

а) Найдите острый угол ВАС между этой хордой и касательной АС к окружности, проведенной через точку А. Ответ дайте в градусах.

б)Найдите длину дуги АВ

Answer 1

Объяснение:

АС-касательная , ∠АСО=50. Найти ∪АВ(меньшую).

ΔОАС-прямоугольный, т.к ОА⊥АС. Найдем ∠СОА=90°-50°=40° ( по св. острых углов).

∠АОВ-центральный, опирающийся на ∪АВ ⇒  ∪АВ=40°

2)

а) Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними⇒∠DFC=36°

б)L=(πrα) :180° ,где  – длина дуги, π = 3,14, r – радиус окружности, α -центральный угол.

∠АОВ-центральный, ∠АОВ=72°,

L=(π*15*72°) :180°=6π≈18,84 (см) .