Question

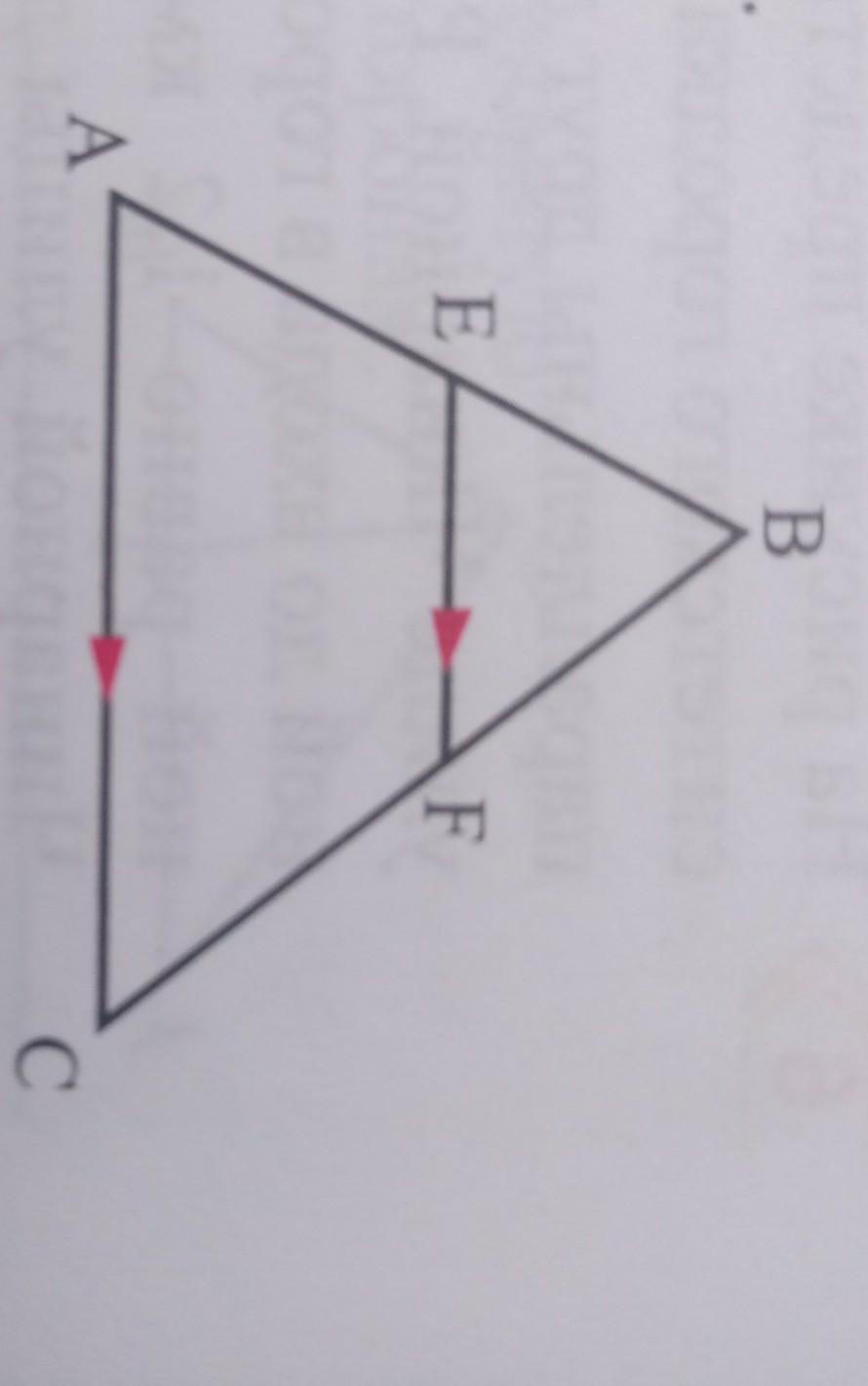
зная,что в уголАВС ||АС найдите требуемое.
а)BE=?,если АВ=64см и ВF:FC=5:3
b)AB=?,если АЕ=18см,ВС:BF=3:2
c)BF=?,Если ВE=12cм,АЕ:FC=4:5
СРЧНОООО ПРОШУ!
дам 25 Балов!!!!
​

Answer 1

В условии задания имеется в виду, что EF║AC.

В решении мы будем использовать теорему о пропорциональных отрезках (или же общую теорема Фалеса):

если угол пересекают параллельные прямые, то отрезки, образованные при этом на одной стороне угла, пропорциональны соответствующим отрезкам на другой стороне.

a)

Дано:

АВ = 64 см;

ВF : FC = 5 : 3

Найти: BE.

Решение:

По теореме о пропорциональных отрезках,

$\displaystyle \frac{BE}{EA}=\frac{BF}{FC}$.

Раз BF относится к FC как 5 : 3 (по условию), то так же относится и BE к EA.

Пусть коэффициент пропорциональности равен x, тогда BE = 5x, EA = 3x.

BE + EA = AB = 64, поэтому можем составить такое уравнение:

5x + 3x = 64

8x = 64

x = 64 : 8

x = 8

BE = 5 · 8 = 40 (см).

b)

Дано:

АЕ = 18 см;

ВC : BF = 3 : 2

Найти: АВ.

Решение:

По теореме о пропорциональных отрезках,

$\displaystyle \frac{BA}{BE}=\frac{BC}{BF}$.

Раз BC относится к BF как 3 : 2 (по условию), то так же относится и BA к BE.

Пусть коэффициент пропорциональности равен x, тогда BA = 3x, BE = 2x.

BA = BE + EA.

3х = 2х + 18

3х - 2х = 18

х = 18

BA = 3 · 18 = 54 (cм).

c)

Дано:

BE = 12 см;

AE : FC = 4 : 5

Найти: BF.

Решение:

По теореме о пропорциональных отрезках,

$\displaystyle \frac{BE}{BF}=\frac{EA}{FC}$.

$\displaystyle \frac{12}{BF}=\frac{4}{5}$.

Для того чтобы найти неизвестный средний член пропорции, нужно произведение крайних членов разделить на известный средний:

$\displaystyle BF = \frac{12\cdot 5}{4}= 15$ (см).

Ответ: а) 40 см; b) 54 см; c) 15 см.