Question

Нужна помощь прошу помочь

Answer 1

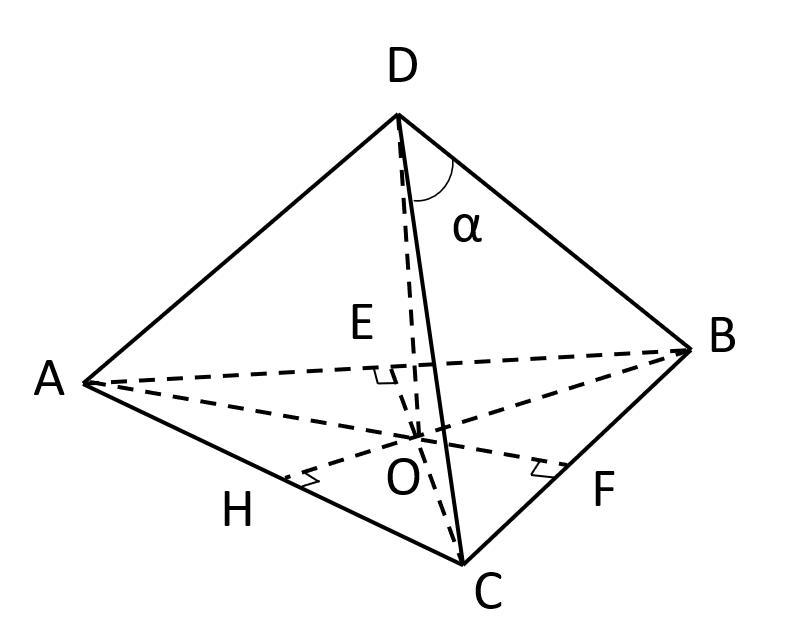
См. рисунок.

Рассмотрим треугольник ABC. В нем точка O - центр, т.е. пересечение медиан, бисектрисс и высот. Поэтому угол ∠HBC=30°.

Из прямоугольного треугольника BOF:

BO=BF/cos30° = 3(√6)/(2√3/2) = 3√2.

Рассмотрим прямоугольный треугольник DOB.

По теореме Пифагора: DB=√(DO²+BO²) = √(36+36) =6√2.

Рассмотрим, наконец, треугольник CDB, он равнобедренный CD=DB=6√2.

Проведем в нем высоту (она является одновременно и бисекриссой и медианой) из точки D в F. FB = CB/2=(3√6)/2.

Тогда, sin (α/2) = FB/DB = (3√6)/(12√2) = √3/4.

Отсюда α/2 = arcsin (√3/4) ≈ 25.65°.

α≈51.3°.