Предмет: Алгебра,
автор: spacesamurai2001
Помогите пожалуйста решить,умоляю
Приложения:
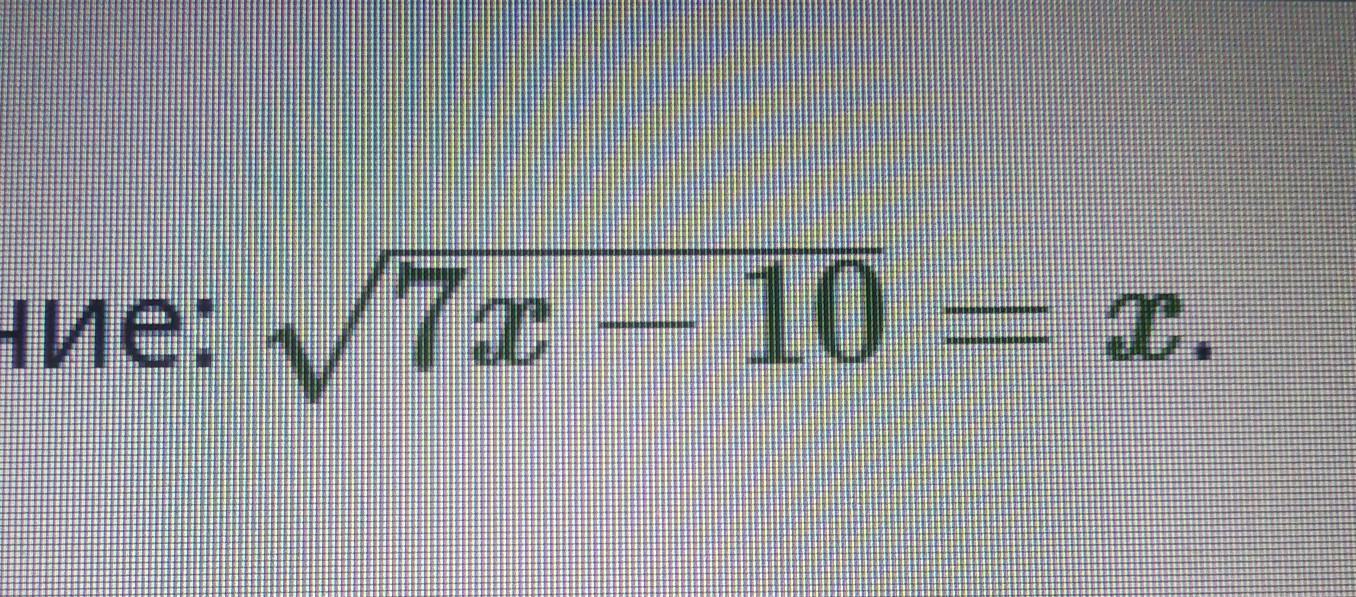
Ответы
Автор ответа:
3
Ответ:
;
Объяснение:
Подкоренное выражение не может быть меньше нуля. Поэтому вычисляем область допустимых значений.
Область допустимых значений:
Теперь решаем уравнение, возведением обеих частей в квадрат:
Universalka:
Почему отмечено нарушение? Отличное решение .
Область допустимых значений подробно расписана
Я не отмечала нарушение
Автор ответа:
1
Возведем обе части уравнения в квадрат, получим квадратное уравнение, решив которое, сделаем проверку, поскольку возведение в квадрат может повлечь появление посторонних корней.
7х-10=х²
х²-7х+10=0, По теореме, обратной теореме Виета х₁=2; х₂=5
Проверка х₁=2; √(7*2-10)=2; √4=2; 2=2- верное равенство.
х₂=5; √(7*5-10)=2; √25=5; 5=5- верное равенство.
Оба корня являются корнями исходного уравнения.
Ответ 2; 5
Похожие вопросы
Предмет: Английский язык,
автор: Маришка5555
Предмет: Русский язык,
автор: misha9998
Предмет: Русский язык,
автор: kseniya28052000
Предмет: Математика,
автор: DaniilHabarov
Предмет: Алгебра,
автор: margaritap2003