Question

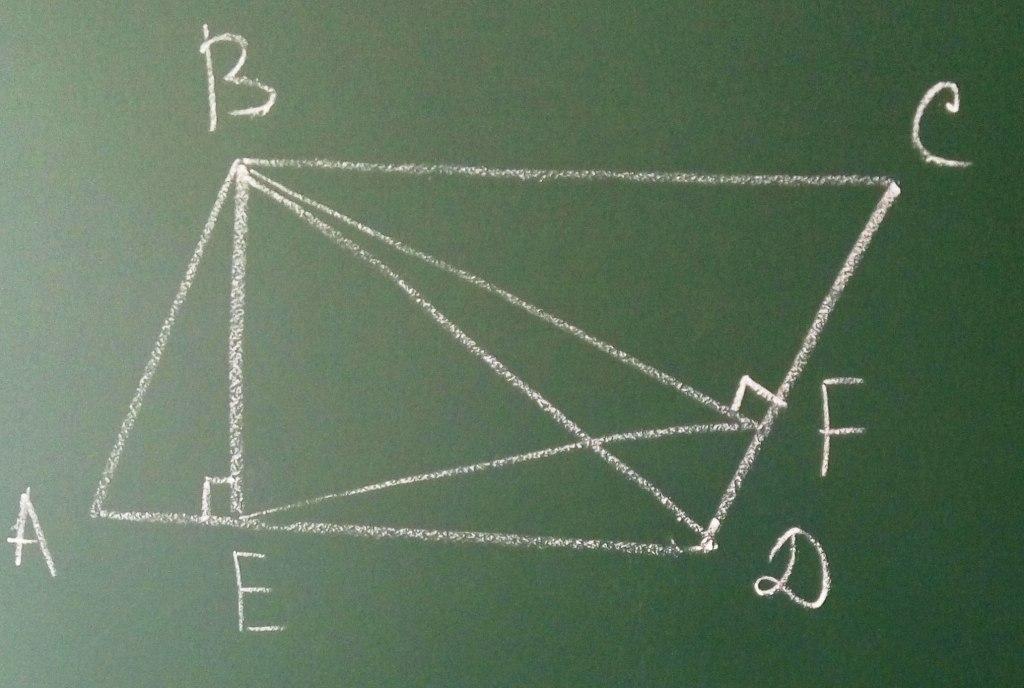
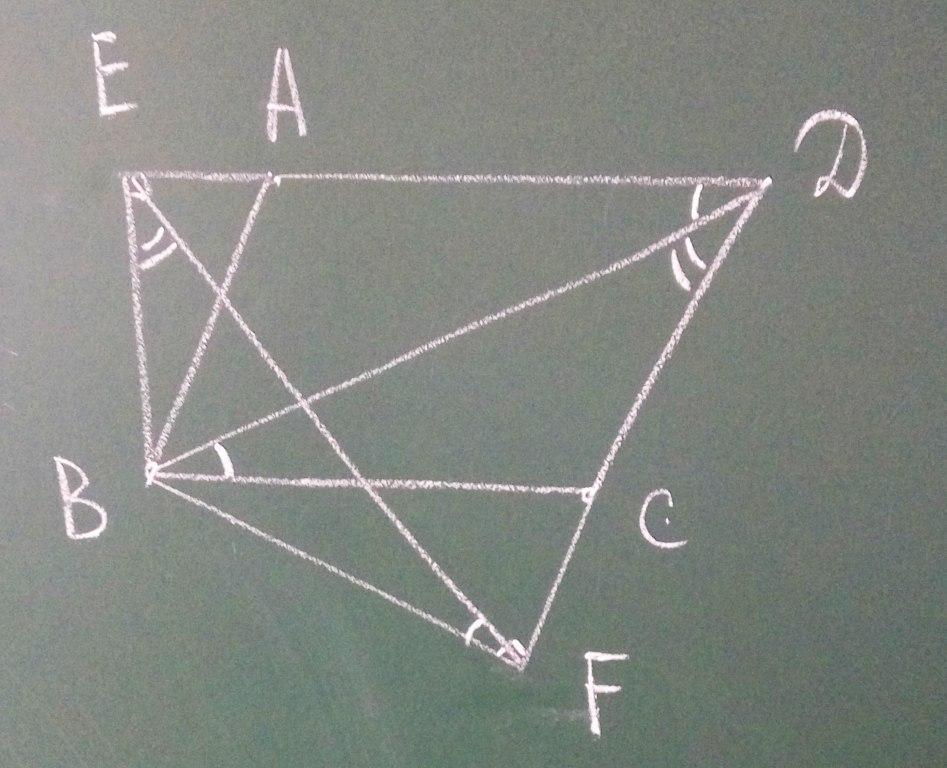
В параллелограмме abcd проведены высоты be и bf к сторонам ad и cd соответственно.
Докажите, что треугольники bef и bdc подобны.
Определите длину отрезка ef, если sinA=0,4 и BD=15
50б,помогите пожалуйста

Answer 1

Ответ:

Объяснение:

ABCD-параллелограмм⇒∠C=∠A, AD║BC

∠C=∠A⇒sin∠C=sin∠A

AD║BC⇒∠CBD=∠ADB

BE⊥AD⇒∠BED=90°

BF⊥AD⇒∠BFD=90°

∠BED=∠BFD=90°⇒ точки B,E,F,D лежат на одной окружности с диаметром BD. Тогда по теореме о равенстве вписанных углов имеем ∠BEF=∠BDF, ∠BDE=∠BFE

∠BFE=∠BDE=∠CBD

∠BEF=∠BDC, ∠BFE=∠CBD⇒ΔBEF~ΔBDC ч.т.д.

Из ΔBEF по теореме синусов имеем EF/sinEBF=2R, где R-радиус описанной окружности около ΔBEF⇒ R=0,5BD, так как это та самая окружность которая содержит точки B,E,F,D.

EF/sinEBF=2R⇒EF=2RsinEBF=BDsinC=BDsinA=15·0,4=6

Случаи того что угол В острый или тупой разбираются аналогично.