Question

Дана правильная четырехугольная пирамида. Боковые грани наклонены к плоскости основания под углом 60°. Сторона основания пирамиды равна 8 см. Найдите площадь полной поверхности пирамиды. С рисунком. Заранее спасибо

Answer 1

Ответ:

Sпол=192 см²

Объяснение:

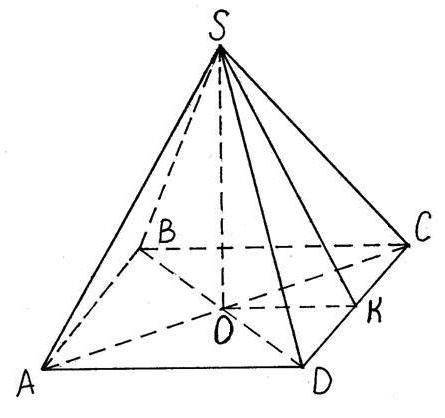
SABCD-правильная четырехугольная пирамида⇒ABCD-квадрат, SA=SB=SC=SD

Проведём высоту SO  и диагонали основания ABCD. Так как пирамида правильная четырехугольная, то AC∩BD=O.

Построим OK⊥CD⇒CK=KD⇒SК⊥CD, так как ΔSCD равнобедренный.

Тогда ∠SKO=(SCD)^(ABCD)=60°.

CD=DK, AO=OC ⇒отрезок KO средняя линия в ΔACD⇒

⇒KO=0,5AD=0,5·8=4

Из прямоугольного ΔSOK   SK=KO/cos∠SKO=4/cos60°=4/0,5=8

Sосн=AB²=8²=64

Sбок=0,5SK·Pосн=0,5·8·4AB=16·8=128

Sпол=Sосн+Sбок=64+128=192 см²