Предмет: Алгебра,
автор: pylypvasylyna
СРОЧНО ПОМОГИТЕ!!!!!!!!!!!!!!!
Очень важно сами шаги решения
Приложения:
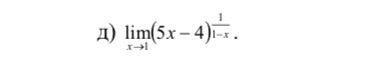
Ответы
Автор ответа:
3
Похожие вопросы
Предмет: Другие предметы,
автор: Veronichka753
Предмет: Українська мова,
автор: Maks3171
Предмет: Русский язык,
автор: Карина0586
Предмет: Литература,
автор: PolinkaNovikova1
Предмет: Математика,
автор: cffghdffhhcf290