Question

11 класс!!! РЕШИТЕ СРОЧНО!!!!!

Answer 1

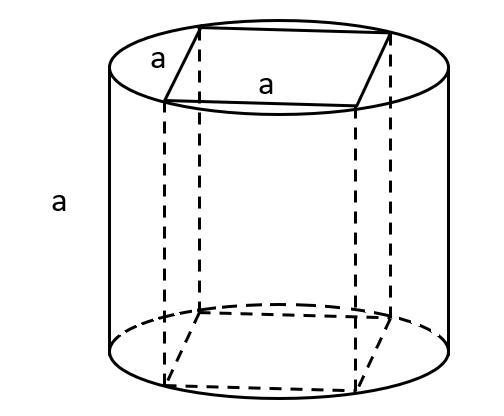
1. См. рисунок.

Ребро куба обозначим a. Тогда и высота цилиндра равна a.

Диагональ грани куба = диаметру, т.е. a√2 = 2R.

Отсюда: R=a/√2

Площадь полной поверхности куба есть 6 площадей граней:

S_куб = 6*S_гр = 6a² = 1024.

Отсюда: a=32/√6

Объем цилиндра: V_цил = S_осн*a = πR²a =πa³/2

$V=\frac{ \pi}{2} \frac{32^3}{6^{3/2}} = \pi \frac{16384}{6^{3/2}}$

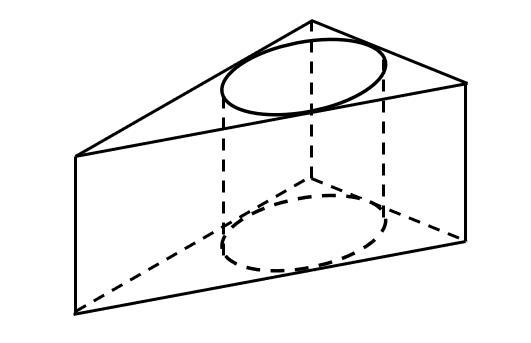
2. См. рисунок.

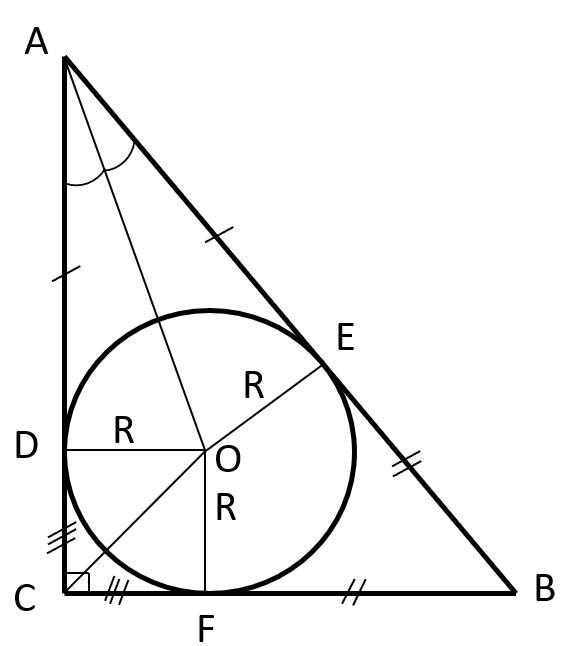
Рассмотрим основание призмы (см. рис.). Прямоугольный треугольник, с катетами AC=8 и BC=6  и гипотенузой AB=√(8²+6²)=10. В него вписана окружность, радиуса R.

Найдем R.

По теореме о вписанной в угол окружности: AD=AE, EB=BF, DC=CF=R.

AD=AC-R = AE = AB-EB = AB - BF =AB - (BC-R)=AB-BC+R

Отсюда: R=(AC+BC-AB)/2=(8+6-10)/2=2.

Объем цилиндра: V=S_осн*H, H-высота цилиндра (и призмы тоже).

S_осн = πR² = 8π/H.

Отсюда: H=8/R² =2.

Площадь боковых граней призмы: S_бок.приз. = H*P, P-периметр треугольника основания.

P=8+6+10=24.

S_бок.приз. = 2*24=48.