найди периметр прямоугольник, если одна из сторон на 2 см больше другой, а радиус описанной окружности равен 5 см
Ответы
Ответ:
28 см
Объяснение:
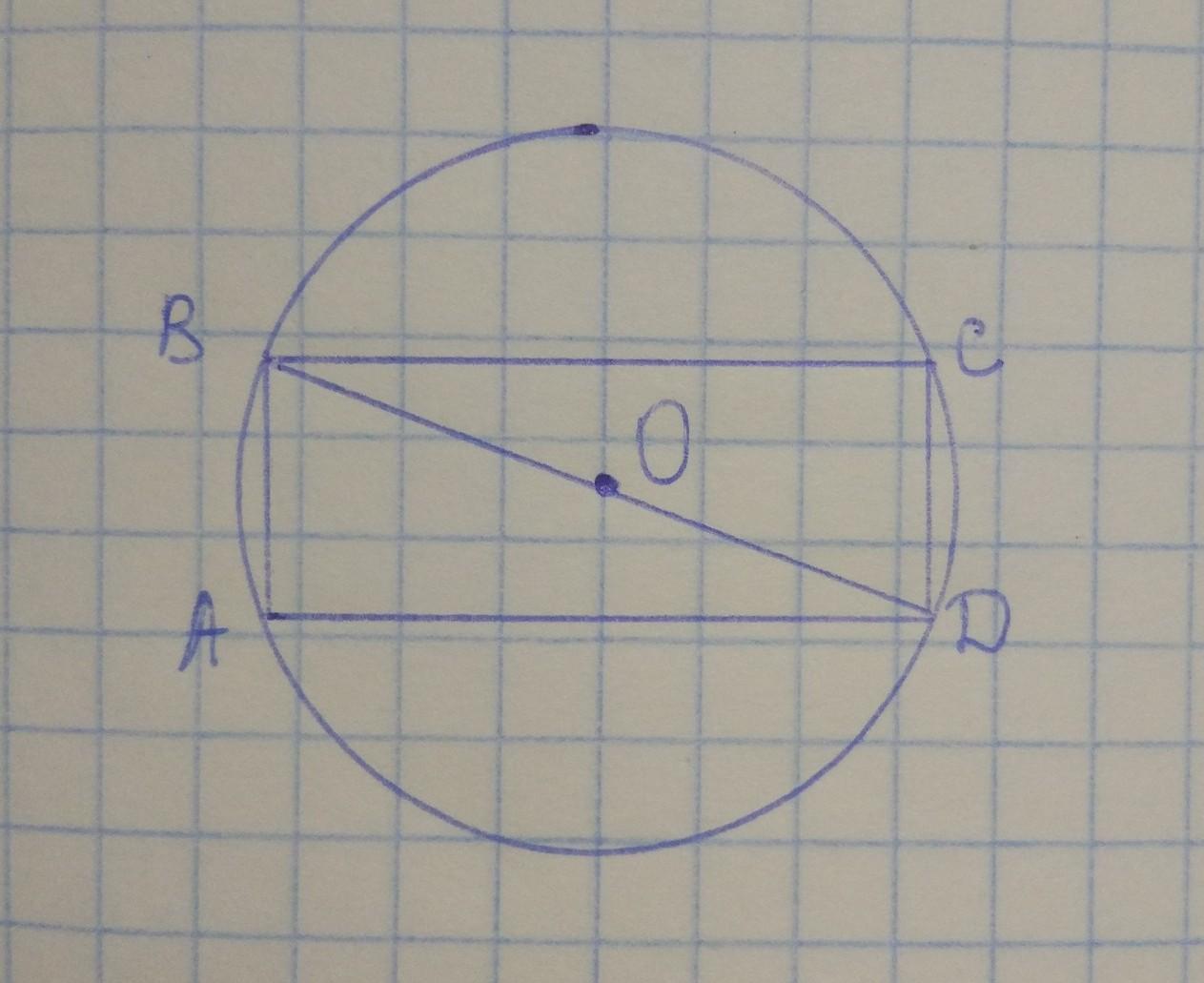
Дано: ABCD - прямоугольник, AD=(АВ+2) см, ω(О; ОА) - описанная, R=5 см
Найти Р
Решение
1) Диагонали АС и BD прямоугольника пересекаются в т. О => OA=OB=OC=OD=R, тогда BD=2R=2OA=5×2=10 см
2) Пусть АВ=х см, x>0, тогда AD=(х+2) см
∆ABD, <BAD=90°, по теореме Пифагора BD²=AB²+AD²
10²=x²+(x+2)²
100=x²+x²+4x+4
2x²+4x-96=0
x²+2x-48=0
По теореме Виета для приведенного квадратного уравнения
{ х1+х2= -b= -2
{ x1x2= c= -48
x1= -8 - посторонний корень, x2= 6 см= AB
AD= x+2= 6+2= 8 см
3) Р= 2(AB+AD)= 2×(6+8)=14×2= 28 см
Ответ:
28
Объяснение:х- меньшая сторона, х+2 большая сторона
Радиус равен 1/2 диагонали, значит диагональ =10.
По теореме пифагора х²+(х+2) ²=10
2х²+4х-96=0 разделим на 2
х²+2х-48=0
По теореме Виета х1+х2=-2
х1*х2=-48. Тогда -8 и 6, -8 не подходит. Х= 6 меньшая сторона, большая сторона равна 6+2=8
Р=2*(6+8) =2*14=28