Question

Помогите решить ...............................

Answer 1

Тут по клеточкам можно высчитать величины определенных отрезков. С помощью прямых треугольников будет находить нужные отрезки.

Нам нужно найти сторону ромба и диагонали, что потом все это подставить в формулу для нахождения радиуса вписанной окружности через диагонали, имеющую следующий вид:

$r = \frac{d_1\cdot d_2}{4a}$,

где а — сторона ромба, d₁, d₂ — диагонали ромба

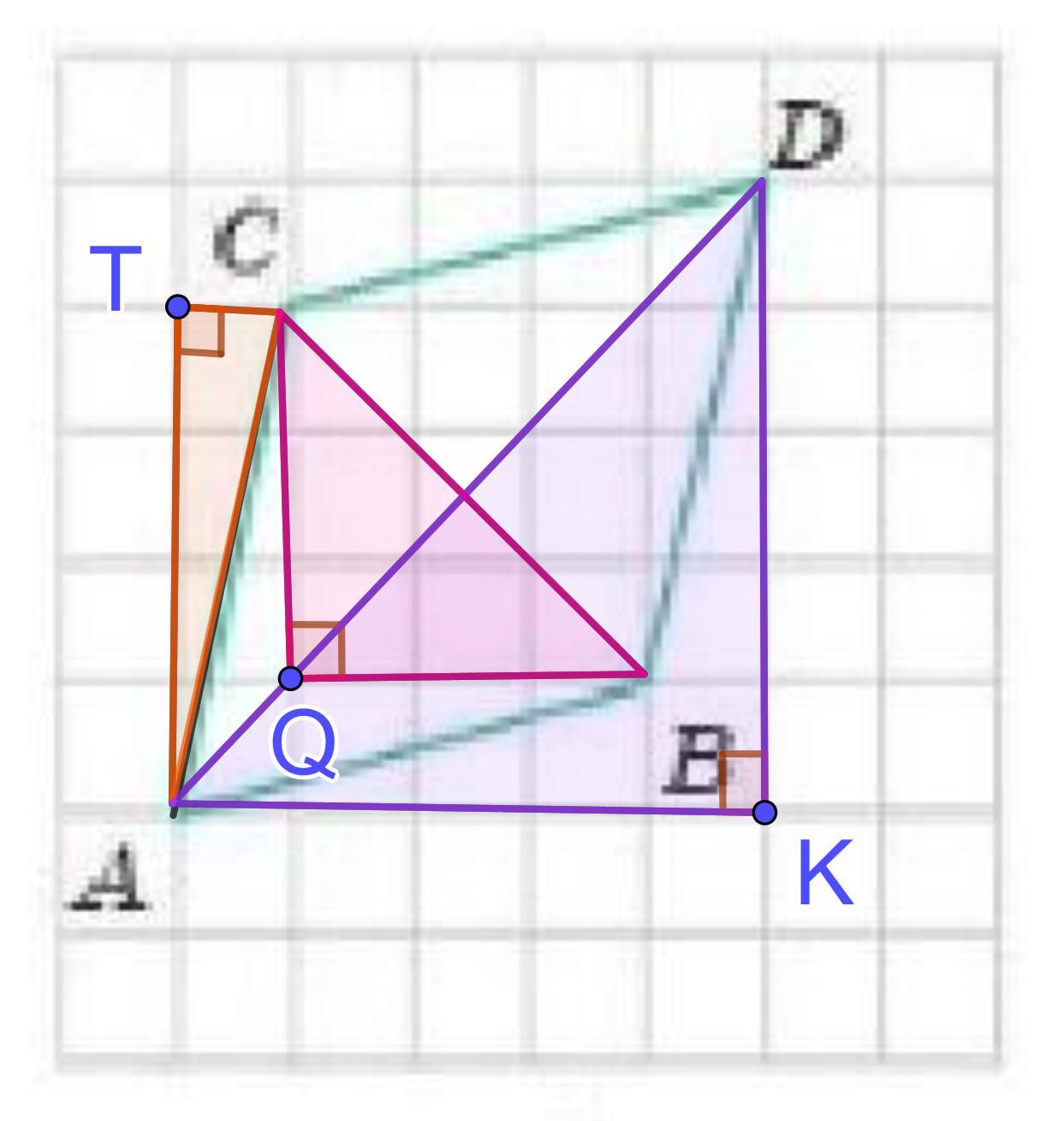
Найдем для начала сторону через ΔACT:

∠ATC = 90°, TC = 4, AT = 1

$AC(a)=\sqrt{TC^2+AT^2} = \sqrt{4^2+1^2} = \sqrt{16+1} = \sqrt{17}$

Найдем первую диагональ через ΔADK:

∠AKD = 90°, AK = DK = 5

$AD = \sqrt{AK^2+DK^2}= \sqrt{5^2+5^2}= \sqrt{25+25} = \sqrt{50}$

Найдем вторую диагональ через ΔCBQ:

∠CQB = 90°, CQ = BQ = 3

$CB = \sqrt{CQ^2+BQ^2}= \sqrt{3^2+3^2}= \sqrt{9+9} = \sqrt{18}$

Подставляем значения в формулу радиуса вписанной окружности через диагонали:

$r = \frac{\sqrt{50} \cdot \sqrt{18} }{4\sqrt{17} } = \frac{\sqrt{900}}{4\sqrt{17} } = \frac{30}{4\sqrt{17} } = \frac{30\sqrt{17}}{4\cdot 17} = \frac{30\sqrt{17}}{68} = \frac{15\sqrt{17}}{34} \approx 1.82$

Ответ: Радиус окружности равен $\frac{15\sqrt{17}}{34}$, что приблизительно составляет 1,82 ед.