Предмет: Алгебра,
автор: zonedd123456789
С объяснением пожалуйста!
Приложения:
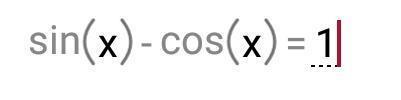
zonedd123456789:
Жаль
Ответы
Автор ответа:
1
Доброго времени суток, извините что Вас отвлекаю, но не могли бы мне помочь? Вопрос: https://znanija.com/task/34818506?utm_source=android&utm_medium=share&utm_campaign=question
Похожие вопросы
Предмет: Русский язык,
автор: Tetradka999
Предмет: Английский язык,
автор: dondiabloz
Предмет: Английский язык,
автор: ndr
Предмет: Литература,
автор: nastycatromcat
Предмет: Математика,
автор: коля630