Найти углы треугольника pts, 100 баллов)
Ответы
Ответ:
∠Т = 50°
∠TPS = 65°
∠TSP = 65°
Объяснение:
Если РТ=TS, то треугольник ΔPTS - равнобедренный.
1) Сумма всех углов четырёхугольника равна: 360°
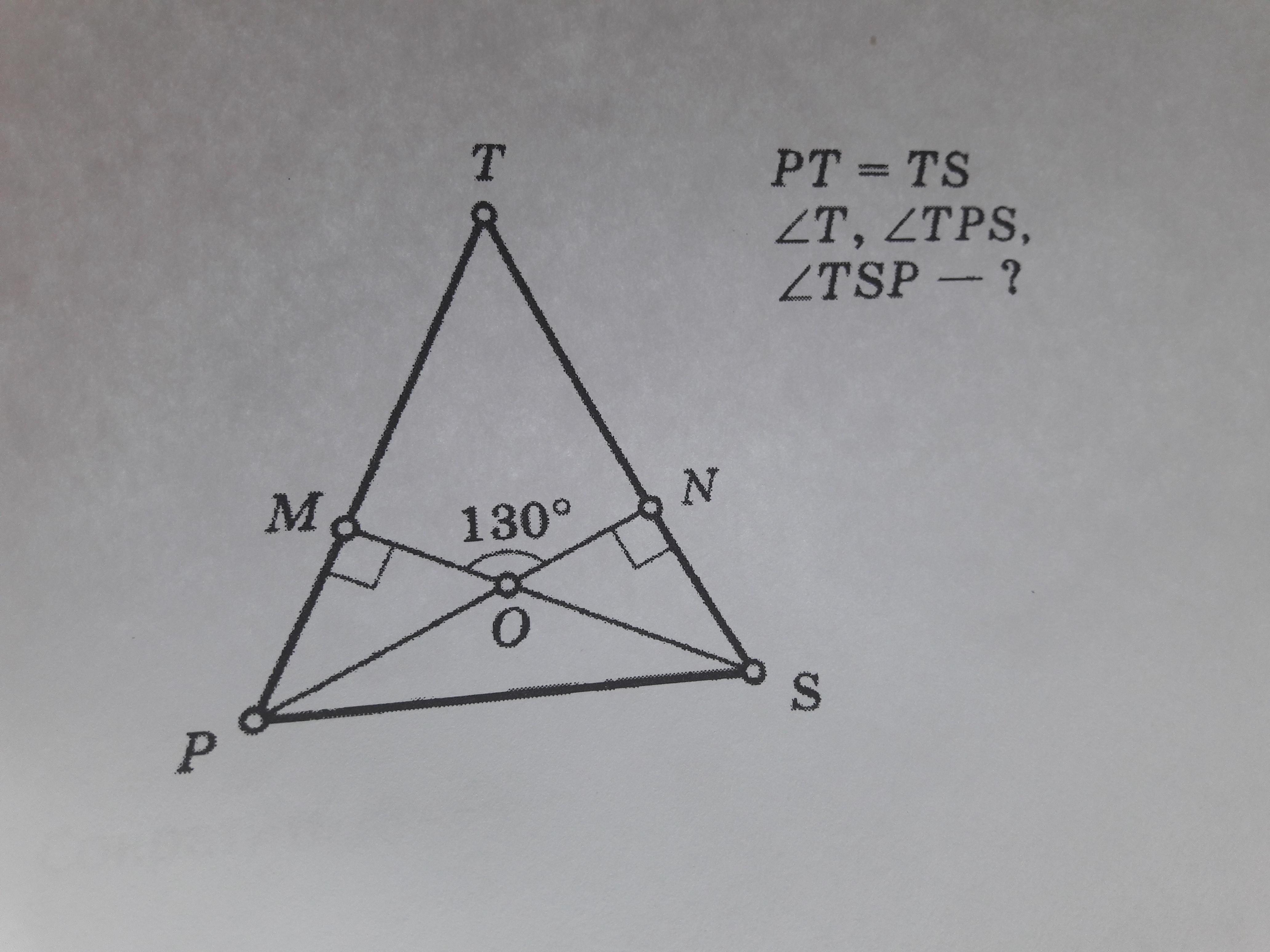
∠TMS = 90°, ∠TNP = 90° как прямые углы, ∠MON = 130° по условию.
Поэтому ∠Т = 360 - 130 - 90 - 90 = 50°
2) ∠МОР = 180° - ∠MON = 180° - 130° = 50° (как смежный углу ∠MON)
3) Сумма всех углов в любом треугольнике равна: 180°
∠PMS = 90° (прямой), поэтому находим угол ∠MPS в прямоугольном треугольнике ΔPMS по сумме всех углов треугольника:
∠MPS = 180° - ∠PMS - ∠МОР = 180 - 90 - 50 = 40°
4) Аналогично находим ∠NSO
∠NSO = 180° - ∠SNO - ∠SОN = 180 - 90 - 50 = 40°
5) Поскольку треугольник ΔPTS - равнобедренный, то их высоты PN и MS также равны и при пересечении в точке О строят два равных треугольника ΔРМО = ΔSNO.
Поскольку углы ∠МРО и ∠SNO равных треугольников равны, то и углы ∠ОРS и ∠ОSР при основании ΔPTS также равны.
6) Сумма 3-х углов треугольника ΔPTS = 180°,
тогда сумма 2-х углов ∠TPS и ∠TSP треугольника ΔPTS:
180° - ∠Т = 180 - 50 = 130°, и поскольку эти углы равны, то каждый из них равен: ∠TPS =∠TSP = 130 ÷ 2 = 65°
7) Т
Ответ:
∠T = 50°, ∠TPS = ∠TSP = 65°.
Объяснение:
В четырехугольнике MTHO ∠Т = 360° - 2·90° - 140° = 50°.
Треугольник PTS - равнобедренный (РТ = TS - дано). =>
Углы при основании равны, сумма углов треугольника равна 180°.
∠TPS = ∠TSP = (180° - ∠Т)/2 = (180° - 50°)/2 = 65°.