Предмет: Алгебра,
автор: marinka31
Докажите неравенство для любых действительных чисел a и b.(задание во вложении)
Приложения:
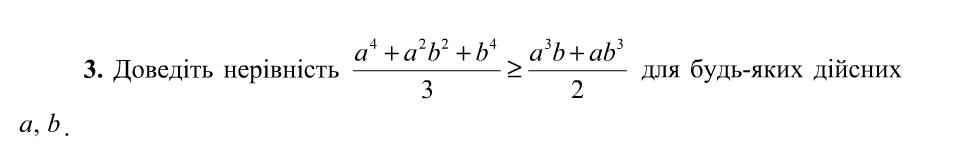
Ответы
Автор ответа:
0
основная идея --- рассмотреть выражение как квадратный трехчлен...
один раз применив замены...
второй раз ---там в конце может быть плохо видно:
2a^2 + 2b^2 + ab ---рассмотрим как квадратный трехчлен относительно а (например...) (можно относительно b рассмотреть ---рассуждения будут похожи...)
2a^2 + b*a + 2b^2 = 0
дискриминант этого выражения всегда <= 0, т.е. корней квадратный трехчлен не имеет, значит ось OX не пересекает, а т.к. это парабола с ветвями вверх, значит она всегда выше оси OX, т.е. неравенство 2a^2 + b*a + 2b^2 >= 0 выполнено всегда...
как-то так...
фото специально не сжимала (долго загружается) ---вдруг будет плохо видно...
один раз применив замены...
второй раз ---там в конце может быть плохо видно:
2a^2 + 2b^2 + ab ---рассмотрим как квадратный трехчлен относительно а (например...) (можно относительно b рассмотреть ---рассуждения будут похожи...)
2a^2 + b*a + 2b^2 = 0
дискриминант этого выражения всегда <= 0, т.е. корней квадратный трехчлен не имеет, значит ось OX не пересекает, а т.к. это парабола с ветвями вверх, значит она всегда выше оси OX, т.е. неравенство 2a^2 + b*a + 2b^2 >= 0 выполнено всегда...
как-то так...
фото специально не сжимала (долго загружается) ---вдруг будет плохо видно...
Приложения:

Похожие вопросы
Предмет: Информатика,
автор: imangalievazhumagul5
Предмет: Английский язык,
автор: Аноним
Предмет: География,
автор: gvvfsbvecvvehvdb
Предмет: Алгебра,
автор: leshakisa