Question

HELP НЕ СДЕЛАЮ УБЬЮТ!
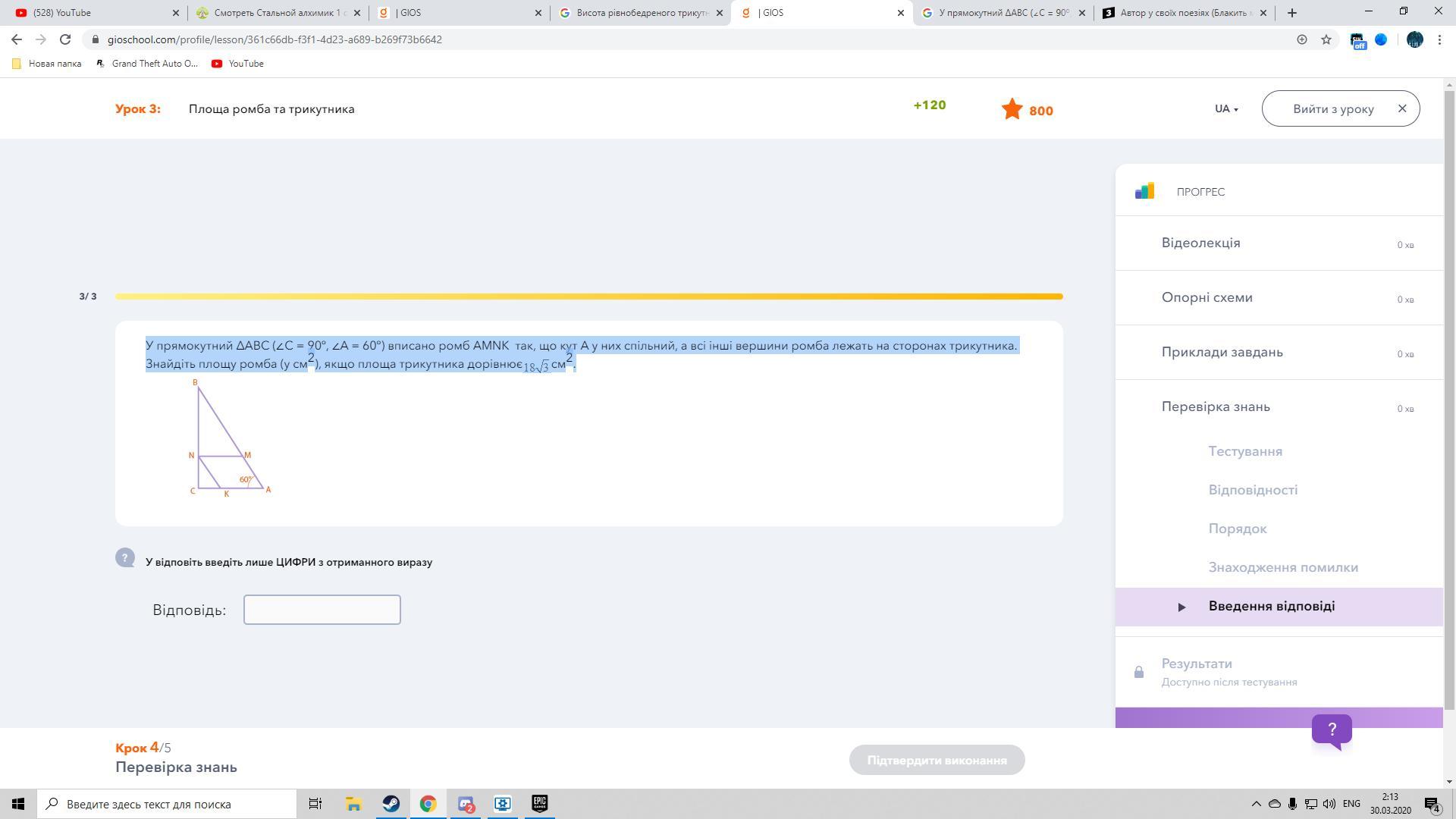
В прямоугольный ΔABC (∠C = 90º, ∠A = 60º) вписано ромб AMNK так, что угол A у них общий, а все остальные вершины ромба лежат на сторонах треугольника. Найдите площадь ромба (в см2), если площадь треугольника доривнюесм2.

Answer 1

ΔАВС - прямоугольный треугольник , ∠С=90° , ∠А=60° , S(АВС)=18√3 .

AMNK - ромб  ⇒   АК║MN  ,  AM║KN  ,  обозначим AK=MN=AM=KN=a .

Так как АК║MN , то ΔMNB - прямоугольный и ∠MNB=90° ,

∠NMB=∠A=60° (как соответственные углы )  ⇒   ∠MBN=90°-60°=30°

Катет, лежащий против угла в 30° :  MN=0,5*ВМ  ⇒  ВМ=2*MN=2а .

BN=√((2a)²-a²)=a√3

ΔKNC:  ∠KNC=∠CNM-∠KNM=90°-60°=30° , так как ∠KNM=∠A как противоположные углы ромба.  Этот факт можно вывести из того , что ΔKNC подобен ΔАВС   ( т.к. АВ║KN ).

Катет КС лежит против угла в 30°, значит равен половине гипотенузы KN=a  ⇒ КС=а/2 .  Катет CN=√(a²-(a²/4))=a√3/2 .

ВС=BN+CN=(a√3/2)+a√3=(3a√3)/2 .

AC=AK+CK=a+(a/2)=3a/2 .

S(АВС)=1/2*АС*ВС=1/2*3а/2*(3а√3/2)=(9√3а²)/8

(9√3a²)/8=18√3  ⇒   a²=144/9  ,  a=12/3=4  .

S(ромба)=а²*sin60°=a²*√3/2=(144/9)*(√3/2)=8√3 .