Question

Помогите пожалуйста!!

Answer 1

Решение смотрите во вложении

Ответ к заданию 3 ВС=4 см, АВ=12-4=8/см/

Answer 2

Тут везде используется свойство угла в прямоугольном треугольнике, где напротив вершины в 30° лежит катет, равный половине гипотенузы.

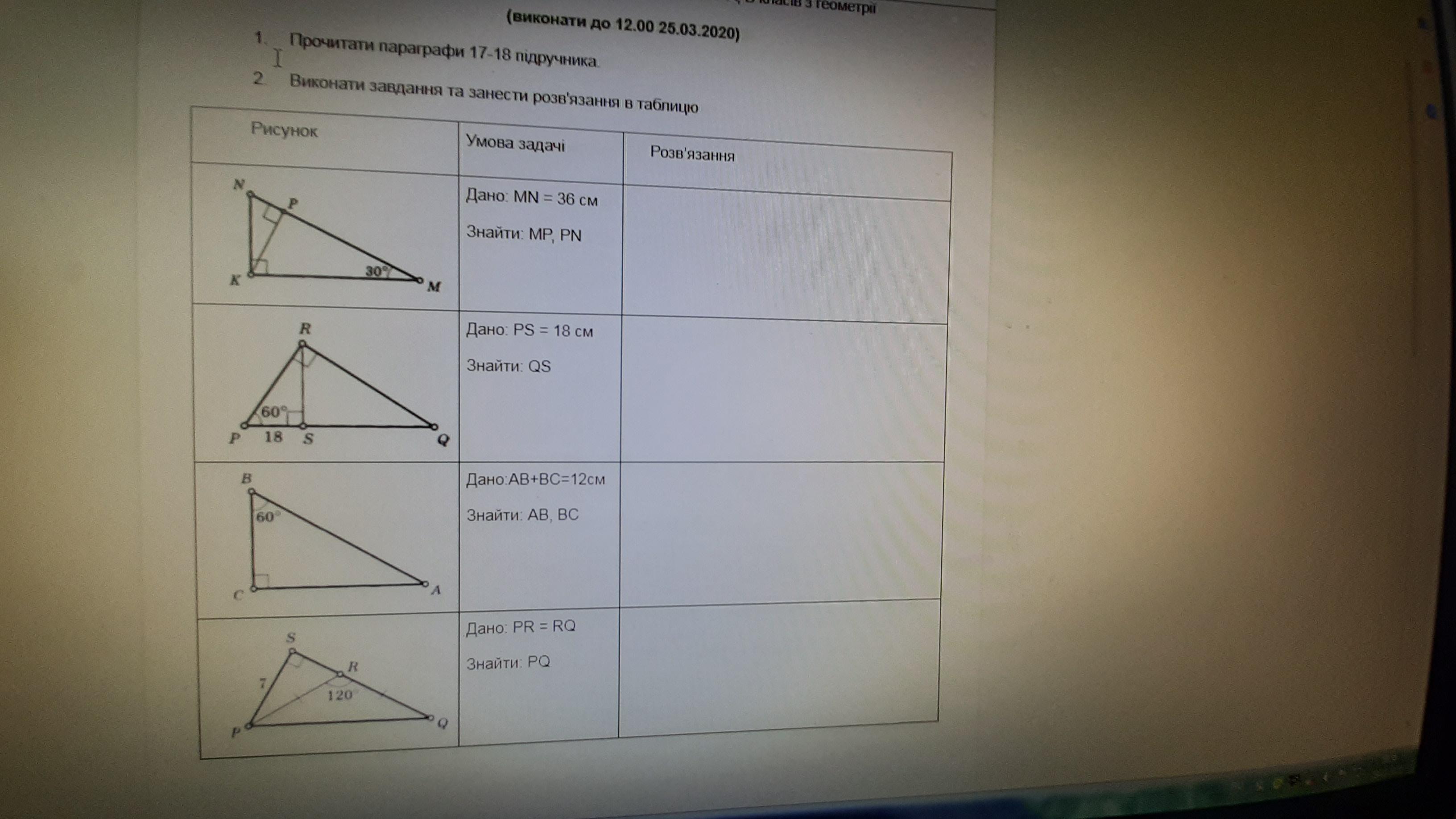
1. Дано прямоугольный ΔMKN, ∠K = 90°, ∠K = 30°, MN = 36 см. Найти МР, PN.

NK напротив 30° ⇒ NK = NM/2 = 18 (см)

∠N = 90−30 = 60°

Р-м ΔKNP:

∠NPK = 90° ⇒ ΔKNP — прямоугольный

∠NKP = 90−60 = 30°

NP напротив 30° ⇒ NP = NK/2 = 18/2 = 9 (см)

Второй катет по т. Пифагора:

$NK^2= PK^2+PN^2 => PK^2= NK^2-NP^2\\PK=\sqrt{NK^2-NP^2}\\PK = \sqrt{18^2-9^2} = \sqrt{324-81}=\sqrt{243}=\sqrt{81}\cdot \sqrt{3} = 9\sqrt{3} \:\: (cm)$

Р-м ΔKPM:

∠KPM = 90° ⇒ ΔKPM — прямоугольный

PK напротив 30°  ⇒  KM = 2*PK = 2·9√3 = 18√3 см.

Второй катет по т. Пифагора:

$MP=\sqrt{KM^2-PK^2}\\MP = \sqrt{(18\sqrt{3} )^2-(9\sqrt{3} )^2} = \sqrt{972-243} = \sqrt{729} = 27 \:\: (cm)$

Ответ: NP = 9 см, MP = 27 см.

2. Дано прямоугольный ΔPRQ, ∠R = 90°, ∠P = 60°, PS = 18 см. Найти QS.

∠Q = 90−60 = 30°

Р-м ΔPRS:

∠PSR = 90°, ∠PRS = 90−60= 30° ⇒

PR = 2*PS = 18*2 = 36 см.

Второй катет по т. Пифагора: $RS=\sqrt{PR^2-PS^2} \\RS=\sqrt{36^2-18^2} = \sqrt{1296-324} = \sqrt{972} = \sqrt{4}\cdot \sqrt{81}\cdot \sqrt{3} = 18\sqrt{3} \:\: (cm)$

Р-м ΔSRQ:

∠RSQ = 90° ⇒ ΔSRQ — прямоугольный

∠SQR = 30° ⇒

RQ = 2*RS = 2*18√3 = 36√3  (см)

Второй катет по т. Пифагора:

$QS=\sqrt{RQ^2-RS^2} \\QS=\sqrt{(36\sqrt{3})^2-(18\sqrt{3})^2}=\sqrt{3888-972}=\sqrt{2916} = 54 \:\: (cm)$

Ответ: QS = 54 см.

3. Дано прямоугольный ΔABC, ∠C = 90°, ∠B = 60°, AB+BC = 12 см. Найти AB, BC.

∠A = 90−60 = 30°

AB = 12−BC

BC напротив 30° ⇒ AB = 2*BC

2BC = 12−BC

3BC = 12

BC = 4  (см)

AB = 12−4 = 8  (см)

Ответ:  АВ = 8 см, ВС = 4 см.

4. Дано прямоугольный ΔPQS, ∠S = 90°, PR = QS, ∠PRQ = 120° PS = 7 см. Найти PQ.

Р-м ΔPQR:

PR = QS  ⇒  ΔPQR — равнобедренный, ∠RPQ = ∠RQP = (180−∠PRQ)/2 = (180−120)/2 = 30°

Р-м ΔPQS:

∠Q = 30°  ⇒  

PQ = 2*SP = 2*7 = 14  (см)

Ответ: PQ = 14 см.