Предмет: Геометрия,
автор: DashaTytka
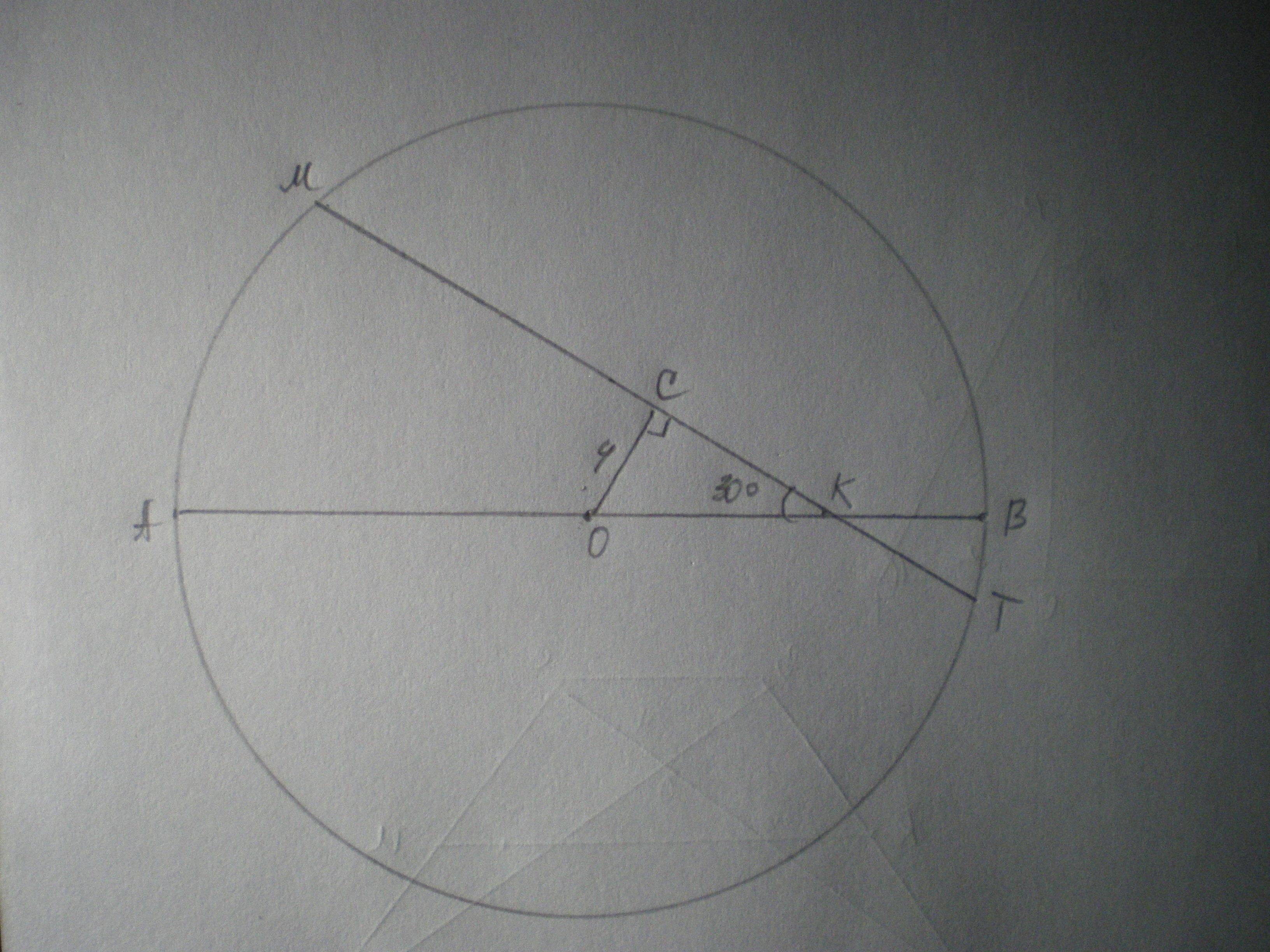
Знайдіть радіус кола, якщо відстань від центра кола до хорди, яка перетинає діаметр під кутом 30° і ділить його на відрізки, пропорційні числам 3 і 11, дорівнює 4 см.
Ответы
Автор ответа:
5
Ответ:
14 см.
Объяснение:
Дано: коло з центром в т. О, АО - радіус, МТ - хорда, ∠АКМ=30°,
КВ/АК=3/11. ОС⊥МТ. ОС=4 см. Знайти АО=ОВ.
ΔСОК - прямокутний, ∠СОК=30°, отже ОК=2ОС=8 см.
Нехай КВ=3х см, АК=11х см, тоді КВ+АК=3х+11х=14х см; АО=ОВ=14х:2=7х см.
ОВ=ОК+КВ; 7х=8+3х; 7х-3х=8; 4х=8; х=2. КВ=3*2=6 см.
ОВ=8+6=14 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: anytkakornyshen
Предмет: Русский язык,
автор: дори1
Предмет: Қазақ тiлi,
автор: aru99
Предмет: Математика,
автор: Ducky6Ninja666
Предмет: Математика,
автор: нукак2