Question

ПОМОГИТЕ УМОЛЯЮ!!!
Биссектриса угла прямоугольника делит его диагональ в отношении 2: 3, а радиус описанной окружности равен см. Найдите площадь прямоугольника.

Answer 1

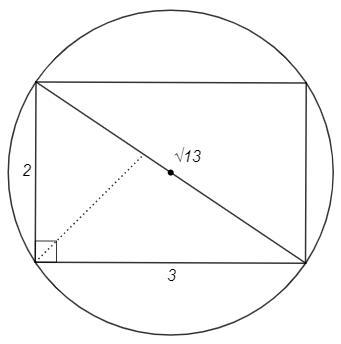
Радиус описанной окружности R (см).

Вписанный прямой угол опирается на диаметр. Диагональ прямоугольника - диаметр описанной окружности, 2R.

Биссектриса делит основание в отношении прилежащих сторон (теорема о биссектрисе). Стороны прямоугольника относятся 2:3. По теореме Пифагора стороны и диагональ относятся 2:3:√13.

S= 2/√13 *2R *3/√13 *2R = 24/13 R^2 (см^2)

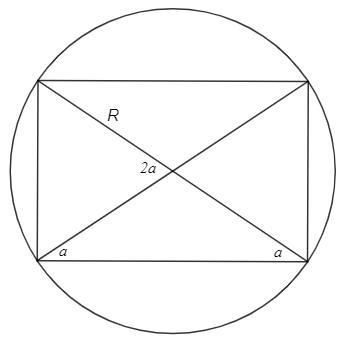
Или по формуле площади четырехугольника

S= 1/2 d1*d2*sinф

tga =2/3

sin(2a) =2tga/(tga^2 +1) =12/13

S= 1/2 *(2R)^2 *12/13 =24/13 R^2

Answer 2

Ответ:    cм →

                                                          https://znanija.com/task/34792852

https://znanija.com/task/34792884

https://znanija.com/task/34793010

https://znanija.com/task/34793026

https://znanija.com/task/34794309

https://znanija.com/task/34794344