Question

ДАНА ОКРУЖНОСТЬ С ЦЕНТРОМ О. НАЙДИТЕ РАССТОЯНИЕ ОТ ЦЕНТРА ОКРУЖНОСТИ ДО ХОРДЫ AB. ЕСЛИ РАДИУС 6СМ

Answer 1

Раз хорда конгруэнтна радиусу, тогда они также равна 6 см.

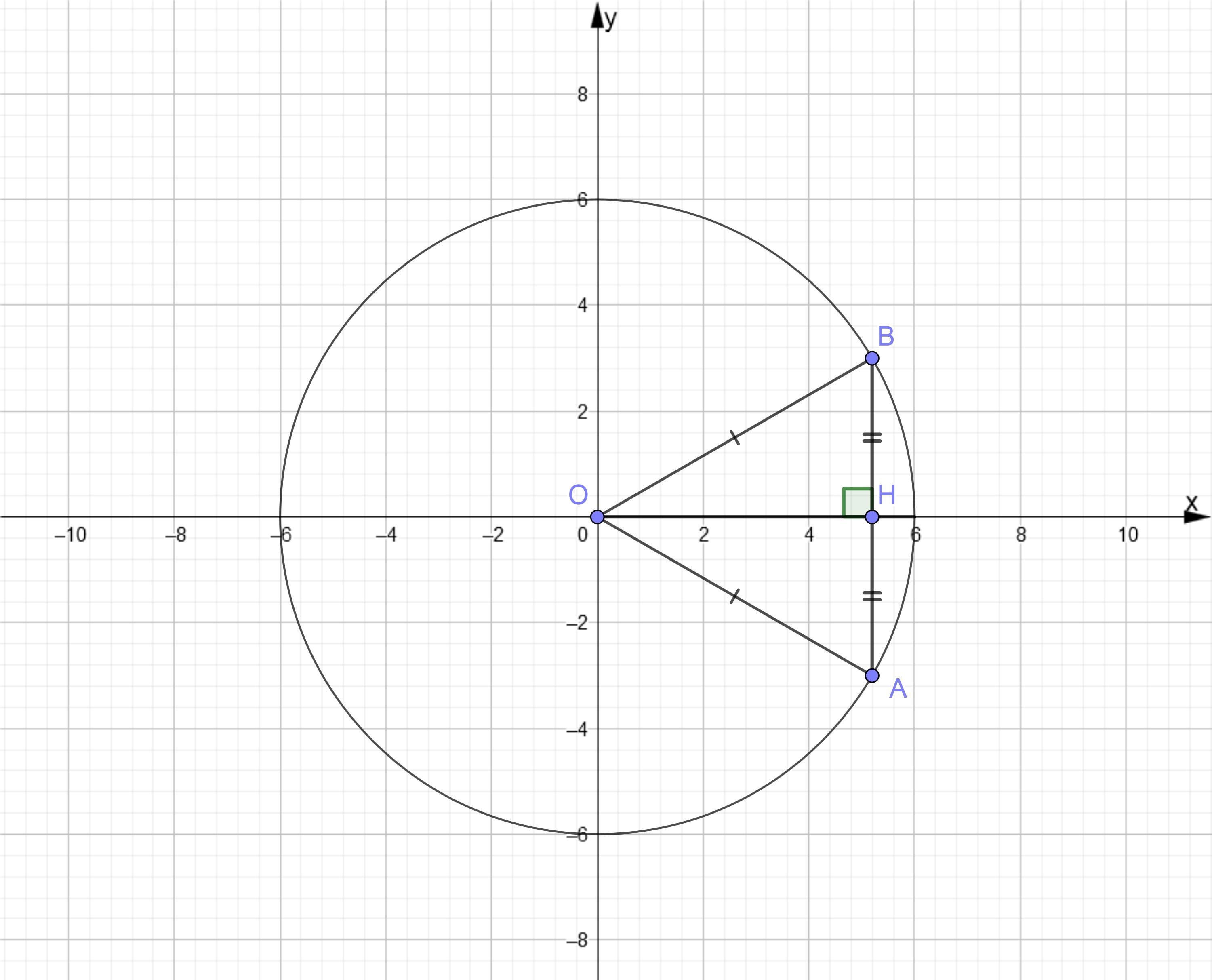
Из центра окружности О проведем перпендикуляр ОH к хорде АВ. Длина перпендикуляра является расстоянием от центра окружности до хорды. OH разделит хорду пополам: АH = HВ = 3см.

Треугольник ОBH — прямоугольный с гипотенузой OB = R = 6 см.

По т. Пифагора:

ОB² = HB² + OH²  ⇒  OH = √(ОB² − HB²)

OH = √(6² − 3²) = √(36 − 9) = √27 = √9·√3 = 3√3 (см)

Ответ: Расстояние от центра окружности до хорды равно 3√3 см.