Предмет: Алгебра,
автор: HopiTakeo
Применяя указанные подстановки, вычислить следующие интегралы:
Приложения:
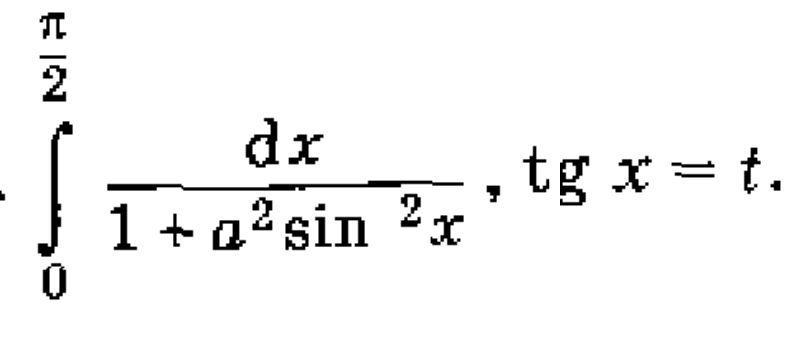
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Решим неопределенный интеграл:
Теперь решим неопределенный интеграл. Подставляя под тангенс, получим бесконечность. Значит мы имеем дело с несобственным интегралом 2 рода. Определим его сходимость:
Интеграл сходится.
Похожие вопросы
Предмет: Английский язык,
автор: эмоВкедах
Предмет: Українська мова,
автор: Seraphim
Предмет: Українська мова,
автор: botiq1
Предмет: Биология,
автор: tashavolkina
Предмет: Алгебра,
автор: sabinamirzoeva1