Предмет: Алгебра,
автор: HopiTakeo
Вычислить интегралы:
Приложения:
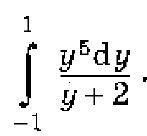
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Разделив на
в столбик, получим:
Похожие вопросы
Предмет: Русский язык,
автор: karinakb
Предмет: Русский язык,
автор: Ольга1880
Предмет: Другие предметы,
автор: DIANAUSA
Предмет: Литература,
автор: kfktnby
Предмет: Математика,
автор: olga9921