Предмет: Алгебра,
автор: HopiTakeo
Вычислить интегралы:
Приложения:
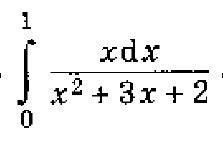
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Разложим дробь в интеграле на простейшие:
Итак:
Похожие вопросы
Предмет: Русский язык,
автор: KристиночкA
Предмет: Английский язык,
автор: dianamelis
Предмет: Қазақ тiлi,
автор: АНЖЕЛА26102000
Предмет: Математика,
автор: аня2256
Предмет: Литература,
автор: hoooooootwdgjy12456