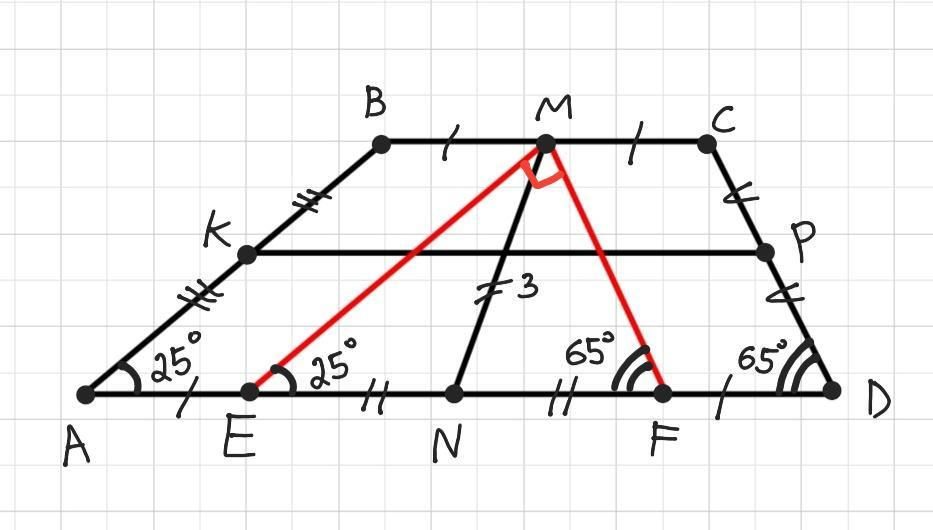
. У трапеції кути при одній з основ дорівнюють 25°і 65°, а довжина середньої лінії - 7 см. Знайдіть основи трапеції, якщо відрізок, що сполучає їх середини, дорівнює 3 см. *
Ответы
Дано: ABCD - трапеція, ВС||AD, KP - середня лінія, KP= 7 см, ∠А= 25°, ∠D= 65°, ВМ=МС, AN=ND, MN= 3 см.
Знайти: ВС, AD.
Розв'язання.
1) Через точку М, що є серединою сторони ВС, проведемо пряму МЕ||АВ і пряму MF||CD. Е∈AD, F∈AD.
∠BAC=∠MED= 25° (як відповідні кути при ME||AB і січній АЕ)
∠CDF=∠MFA= 65° (як відповідні кути при MF||CD і січній FD)
2) Оскільки ME||AB і BC||AD, то ABME - паралелограм, АЕ=ВМ.
Оскільки MF||CD і BC||AD, то FMCD - паралелограм, MC=FD.
AE=BM, MC=FD, BM=MC => AE=FD => BC=BM+MC= AE+FD => AD=BC+EF.
3) Розглянемо ΔEMF.
∠MED= 25°, ∠MFA= 65° => ∠EMF= 180°–(25°+65°)= 90° (сума всіх кутів трикутника 180°).
Отже, ∠EMF=90° => ΔEMF - прямокутний.
4) Оскільки AN=ND і AE=FD, то EN=NF => MN - медіана ΔEMF.
В прямокутному трикутнику медіана проведена до гіпотенузи дорівнює половині гіпотенузи. Тобто MN=EN=NF= 3 см. Звідси EF=EN+NF=3+3= 6 см.
5) Середня лінія трапеції дорівнює половині суми її основ.
КР= (BC+AD):2;
BC+AD= 2KP.
За умовою КР= 7 см, AD=BC+EF= BC+6.
Тому:
ВС+ВС+6= 14;
2BC= 8;
BC= 4 (см).
Тоді AD=4+6= 10 см.
Відповідь: 4 см, 10 см.
P.S. А баллов все-таки мало Вы дали :)