Предмет: Алгебра,
автор: ivandenzzi
Найти точку максимума/минимума и наибольшего/на меньшего значения функций.
Приложения:
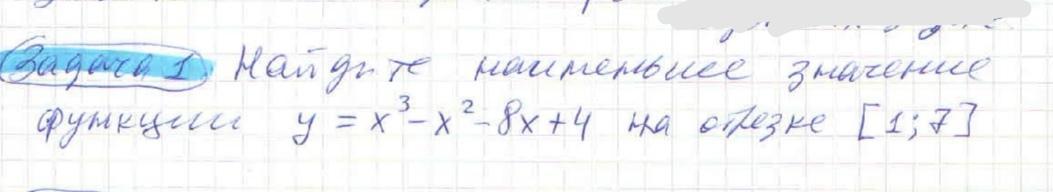
Ответы
Автор ответа:
1
Ответ:
y=x^3-x^2-8x+4
y'=(x^3-x^2-8x+4)' = 3x^2-2x-8
3x^2-2x-8=0
D=4-4*3*(-8)=4+96=100
x1=(2-10)/(2*3)=-8/6=-4/3
x2=(2+10)/(2*3)=12/6=2
Производная при ( - оо ; -4/3) положительная
Производная при ( -4/3 ; 2) отрицательная
Производная при ( 2 ; +оо) положительная
х (max) = -4/3; x(min) = 2
На отрезке [1;7] функция от 1 до 2 убывает, от 2-х до 7 возрастает.
Наименьшее значение функции y=x^3-x^2-8x+4 на отрезке [1;7] будет:
y(2)=2^3-2^2-8*2+4= 8-4-16+4=-8
Похожие вопросы
Предмет: Русский язык,
автор: Katty129
Предмет: Русский язык,
автор: DiKaA
Предмет: Русский язык,
автор: Katty129
Предмет: Литература,
автор: nastashishkina5
Предмет: Алгебра,
автор: albinasupper204