Question

ПРОШУ ПОМОГИТЕ!!!!!!
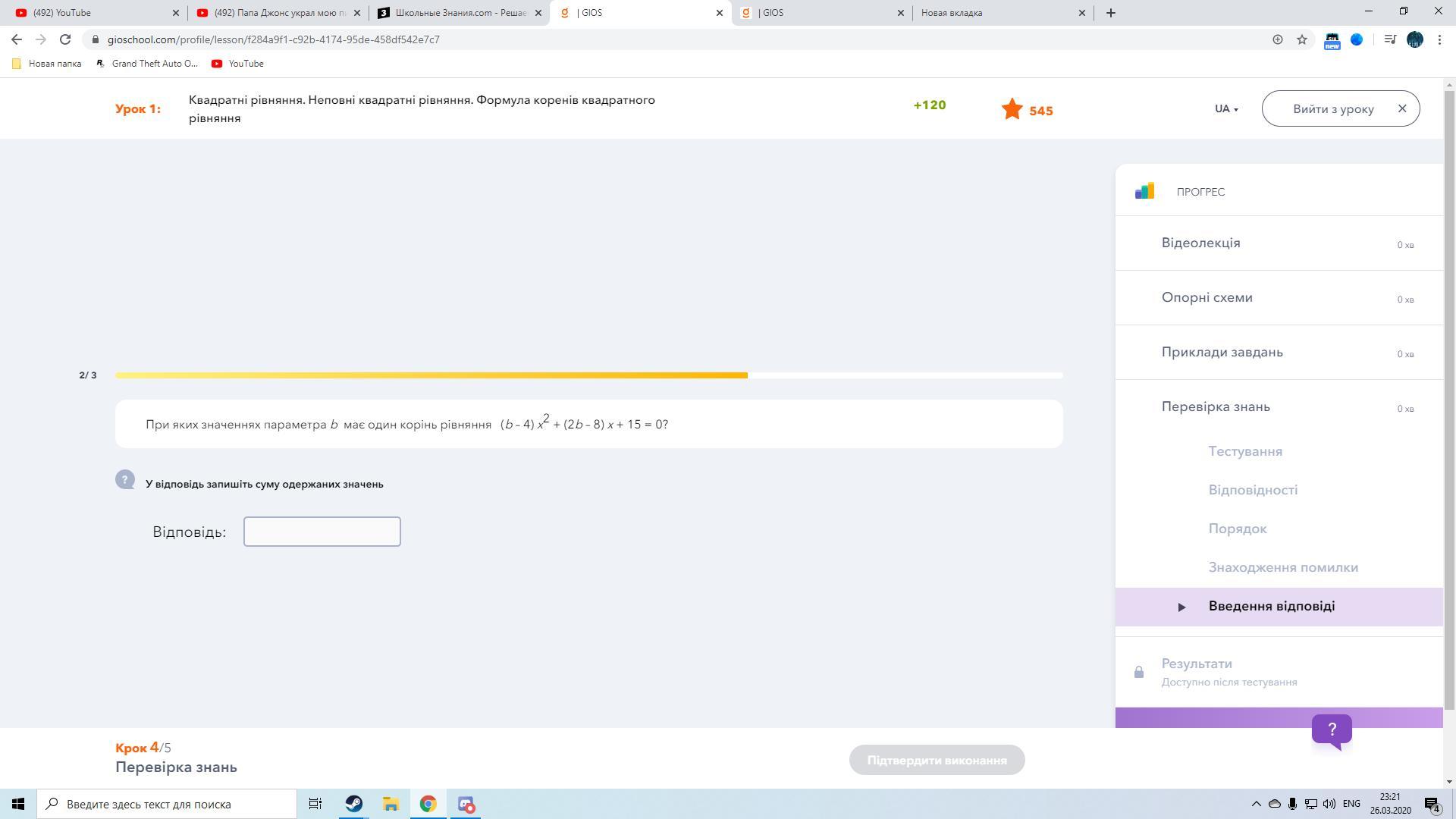
При каких значениях параметра b имеет один корень уравнения

Answer 1

Ответ:

19

Объяснение:

(b-4)x²+(2b-8)x+15=0

1) b-4=0⇒ 15=0⇒ корней нет

2) b-4≠0

D= (2b-8)²-4(b-4)·15=4b²-32b+64-60b+240=4b²-92b+304

Уравнение имеет ед.корень⇔D=0⇒4b²-92b+304=0

4b²-92b+304=0

b²-23b+76=0

По теореме Виета

b₁+b₂=-(-23)=23

Правда здесь получим противоречие. b=4 один из корней полученного уравнения. А выше было показано, что в этом случае корней данное уравнение не имеет. Так что правильный ответ должен был быть 19